APL87
Kenneth E. Iverson
I.P. Sharp Associates
I first began developing a formal language for use in teaching in the graduate program in Automatic Data Processing established by Professor Howard Aiken at Harvard in 1955. This language, now known as APL, has since passed through several phases, the main ones being documented in three publications [1-3]; my book A Programming Language in 1962, the APL\360 manual in 1968, and the APLSV manual in 1975. The last two were co-authored with A.D. Falkoff.
The specifications of the language provided by these publications were later supplemented by more philosophical studies that discussed the design principles followed, and the major design choices made. These include The Design of APL [4], and the Evolution of APL [5], by me and Falkoff, and The Story of ○ , by E.E. McDonnell [6].
Because of implementations produced by various manufacturers, and because of attempts to inject aspects of other languages (as in APLGOL), many diverse lines of development have been pursued. These have been largely reported in manuals, in the proceedings of APL conferences, and in journals such as APL Quote-Quad (Association for Computing Machinery), and Vector (British Computing Society).
In 1978 I began a line of development which has been reported largely in documents internal to IBM Corp. [7] and to I.P. Sharp Associates [8-10], but also in APL conferences [12-13]. This work has culminated in A Dictionary of APL, scheduled to appear in an early issue of APL Quote-Quad [14]; in what follows it will be referred to as “the dictionary”.
The present paper is a companion study in the manner of [4-6]. A preview of it was presented in November of last year at an internal IBM conference that commemorated the 20th anniversary of the initiation of the APL timesharing service within IBM.
The major points to be discussed here include terminology, the APL alphabet, word formation, parsing rules, mixed functions, operators, and localization. In discussing decisions made in the early days by me and colleagues in the APL group in the T.J. Watson Research Center, (notably A.D. Falkoff and L.M. Breed), I will use the term we; this usage is not meant to imply their agreement with the current thinking of myself and present colleagues at I.P. Sharp Associates as presented in the dictionary.
Although there is no current implementation of the entire
dictionary, several implementations embody significant parts of
it, such as the application of operators to derived and user-defined
functions, and the production of “mixed” arrays by expressions
such as 3 4 5, 'ABCD' .
Two implementations
[13,
15]
are particularly close to the dictionary;
the latter was used in all executed examples in this paper.
A. Terminology
Except for the use of brackets, branches, comments, and diamonds (to be discussed and dismissed later), all of the parts of speech of APL are illustrated in the following sentence that defines factorial n :
×/+\(n←5)⍴1
Because of our familiarity with mathematics and computers, we chose terms for them as shown on the left below, although the analogous terms from English are more apt and revealing:
| Variable or constant | n 5 1 | Pronoun or noun | ||
| Function | × + ⍴ | Verb | ||
| Operator | / \ | Adverb | ||
| ( ) | Punctuation | |||
| Assignment | ← | Copula or verb-to-be |
Faults in the chosen terminology are easily seen: as in the illustrative sentence, there is commonly nothing variable in the use of a name; though perhaps apt when first chosen, function no longer strongly suggests the sense of to do or to perform implicit in its Latin root fungi; operator, in the appropriate sense used by Heaviside is less commonly known than is the use as a synonym for function; no part of speech is specified for the parentheses; and assignment suggests the underlying mechanics of the computer rather than the straightforward notion of is, which implies that n←5 be read as “n is 5”.
Because the term programming has come to be associated primarily with the execution of algorithms, and because APL is also used as an analytic notation, the “P” occurring in the acronym APL has often been criticized as too restrictive. However, it should be recalled that the analytical use of APL was emphasized from the outset, as in the following sentence from the preface of [l]:
Chapter 7 (The Logical Calculus) emphasizes the formal manipulability of the language and its utility in theoretical work.
Moreover, since the root meaning of the word “program” is simply “to write in advance”, the acronym APL still seems to be appropriate. However, APL should be characterized as a language that is both analytic and executable, as contrasted with mathematical notation that is analytic but not executable, and with most programming languages that are executable but not analytic.
Terms used for primitive verbs should often be varied to suit
the context, as suggested in the table of standard names and
synonyms of the dictionary; in non-mathematical contexts. the
terms list and table should be preferred
over vector and matrix.
The use of the phrase “shared name” in the dictionary implies
a substantive change, implying that sharing is not restricted to
the names of “variables”
or “nouns” as in current APL systems.
B. Alphabet
In designing an APL alphabet for the 88-position typing element of the Selectric-like IBM 2250 terminal, we adopted the fruitful notion of composite characters formed by overstrikes. Nevertheless, space remained for only one case of the English alphabet; we chose majuscules as more distinct from our other symbols, but chose to place them in the lower-case position, anticipating more use of them than of other symbols.
Demand for a second case (first motivated by an attempt by John Lawrence and his colleagues in SRA to use single-character identifiers on a tiny APL machine) led us to produce one by overstriking the English alphabet by an underscore. This rather awkward and ugly solution proved so satisfactory that experienced APL users tend to reject the straightforward use of miniscules and majuscules (in their normal lower and upper-case positions) made possible by machines such as the IBM PC, and adopted in the form shown in Appendix A.
We designed the special APL characters by simply selecting and modifying characters from various fonts; the appearance could now be much improved by a professional re-design as discussed by Tuttle [16].
There is still a need to make APL usable
from normal ASCII keyboards.
Most attempts to fill this need are based upon
choosing names for the functions represented
(commonly including distinct names for monadic and dyadic cases),
and therefore lose the mnemonic associations designed into the
symbols themselves. An alternative solution, illustrated by the
table in Appendix B
reproduced from the dictionary,
approximates the appearance of the symbols themselves,
and is therefore directly readable by anyone familiar
with the proper symbols.
C. Word Formation
In natural languages, word-formation and parsing are viewed as distinct processes. In APL, as in most programming languages, the two were lumped together in what was misnamed “syntax” with the result that the essentially simple and static rules of word-formation became somewhat confused. For example, the phrase 2e5 was treated as a single word, but in some implementations 2j5 was treated as two words (the number 2 and the function name j5 ). The introduction of complex numbers then caused problems, since it became essential to treat 2j5 as a single word.
A simple and systematic word-formation rule, specified formally and informally in the dictionary, leads to the introduction of new classes of words that could be adopted for use as names or constants. For example, 31416abc3 could denote the name abc3 in file 31416 , and 2r3 could denote the constant rational 2÷3 . Until so adopted, new words would yield value errors when used.
The formal definition of word-formation given in the dictionary is reproduced below:
words:f(c g(q∧¯1↓0,q←∨⌿3↑c)⍱q∧¯1↓0,q) 1⍤<,⍵⊣
q←q∨≠\q←,¯1↑c←(<,⍵)∊⍤>P
f:(0≠,⍴⍤>c)/c←(r⊥⍤>r←⌽¨>a)↓¨>(-a⊥⍤>a←⍵=¨>' ')↓¨> ⍵
g:⍵\(q⍲¯1↓0,q←⍵/(∨⌿⍺[1 3;])∨(⍺[2;])∧1↓(∨⌿⍺[1 2;]),0
The parameter P is a 5-element list of boxed lists consisting
of the quad (⎕) and
the native alphabet, the
macron (¯) and
the decimal digits, the period (.), the
space, and the quote (').
D. Parsing
The parsing rules of APL were complicated significantly by constructs such as mixed output, bracket-semicolon indexing, comments, and diamonds, which do not obey the normal rules for the five parts of speech discussed in section A. I will first discuss the parsing rules for the five parts of speech and then discuss the reasons for introducing the anomalous constructs, and the facilities proposed to supersede them.
Excluding the anomalous constructs cited, the parsing rules of early APL were simply stated. They are adopted in the dictionary with the added proviso that an adverb applies to the result of the entire verb phrase that precedes it.
The corresponding formal rules (also given in the dictionary) concern the selection from the first four elements of the execution stack of a phrase to be executed and replaced by its result. The process is controlled by an 8 by 4 table of cases.
The indexing we desired required an index list of arbitrary ranks to select along successive axes. Since the language as then conceived embraced no such entity, we chose to use a pair of enclosing symbols (the brackets) to indicate that the enclosed phrase was to be treated as a single entity under somewhat different rules than normal. The later introduction of the “enclose” or “box” function has made such lists a part of the language and provided the basis for an indexing function such as the “from” function defined in the dictionary; it follows normal rules and provides indexing that is more convenient and general than that provided by the older form.
For example if i←<¨>⍳1↑⍴A and j←<¨>i , then i{A selects each of the major cells of A , and j(A selects the “complementary” cells. Consequently, the determinant function (the monadic case of -.× as defined in the dictionary) can be defined recursively as:
DET: (0{⍵)-.×DET j{⍵: 0=⍴j←<¨><¨>1↓⍳1↑⍴⍵ : ''⍴⍵
The use of ⍝ and ⋄ can be superseded by the lev and dex functions proposed long ago by Trenchard More, and adopted in the dictionary as left and right, denoted by ⊣ and ⊢ . The following discussion is taken from Section E of the dictionary:
Anything following a comment symbol (⍝) in an expression is ignored in its execution. Comment can be similarly added to the end of a line by appending ⊣'This is a comment' , but can also be inserted anywhere in a line. Thus:
⍺←⍵× ⊢'count to n'⊢ ⍳n←'length of r'qltack ⍴rExpressions using the statement separator (⋄) can be mimicked by expressions using the function left, the primary difference is that the separation imposed by ⊣ follows the normal rules for order of execution. For example, either of the following expressions will determine the coefficients c of a polynomial equivalent to a polynomial with roots r :
n←⍴r⋄b←n⍴2⋄t←b⊤⍳×/b⋄s←(⍳1+n)∘.=+⌿t⋄p←r×.*t⋄c←s+.×p c←s+.×p⊣p←r×.*t⊣s←(⍳1+n)∘.=+⌿t⊣t←b⊤⍳×/b⊣b←n⍴2⊣n←⍴rSince ⊣ is a normal function with simple properties, the phrase b⊣b can be simplified to b , and (since p is used nowhere else) the phrase p⊣p← can be omitted entirely, allowing the second expression to be simplified to:
c←s+.×r×.*t⊣s←(⍳1+n)∘.=+⌿t⊣t←b⊤⍳×/b←n⍴2⊣n←⍴rIt should also be remarked that left can be used to avoid the use of parentheses to any desired degree, as in s*.5⊣s←+/a*2 , and that the symbol ⊣ may then be read as “where” in the sense used in mathematics; that is, “the square root of s , where s is the sum of the squares of a ”.
E. Mixed Functions
In designing the so-called mixed functions, we attempted to achieve the same sort of systematic extension to higher-rank arrays implicit in the scalar functions. Unfortunately, we did not hit upon a unifying principle for such extensions.
The notion of verb rank provides such a principle: each verb has a specified rank, and a verb of rank k applies to each of the k-cells of an argument a (where the k-cells of a are the cells of shape (-k)↑⍴a ), producing a result of shape ((-k)↓⍴a),s , where s is the common shape of the results of applying the function to each of the k-cells. Consequently, a function need be defined only on its k-cell, a circumstance that contributed greatly to the brevity of the dictionary. For example, reversal can be defined by merely stating its rank (1) and defining it for the simple case of a vector (as by the example ⌽'abc' ←→ 'cba' , since all functions extend to higher rank in the same simple manner.
Specification of the rank of a function is also fruitful. For example:
a←2 3 4 ⍴ ⍳ 24 ,⍤2 a 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 0 1 2 ⌽⍤0 1 'abc' abc bca cab
F. Operators
Having hit upon the notion of operators, we were aware of the possibility of introducing such useful cases as composition, dual, and derivative; but other matters were more pressing and their introduction has only begun relatively recently.
One opportunity we failed to recognize was to produce a defined function by applying an operator rather than a function (⎕fx) to the canonical representation. Such an operator is defined in [14]; briefly, m∇d produces an unnamed ambivalent function (with the monadic and dyadic cases being determined independently by the vector-of-vectors representations m and d ). The unnamed function may be applied directly, as in m∇d a , or assigned a name, as in f←m∇d or (f←m∇d) a .
To allow for recursive definition in an unnamed function,
a symbol is provided for self-reference in the representation.
This scheme makes possible safe and simple reassignment
of the name of a recursively defined function, something not
possible in the case of a function defined
by ⎕fx .
A symbol is also provided for the instruction counter,
so that branching is
indicated by a normal use of assignment.
G. Localization and Assignment
In designing a canonical representation for functions, we chose to specify localizations by a list of names in the header. Users soon suggested a converse scheme of listing the globals and localizing all names not listed. Although this scheme offered some convenience, we rejected it on the basis that the names of all supporting defined functions used would have to be listed in the header, introducing an unnecessary distinction between the uses of primitives and defined functions and therefore, to some degree, discouraging the use of structured programming.
About 1970, Orth and I adopted [17, 18] a scheme called direct definition, in which a name was localized if it appeared to the left of an assignment arrow. This was later refined to provide control of localization: a name was local if it occurred immediately to the left of ← , so that a←3 localized a , but a ←3 did not.
The scheme in the dictionary differs in two significant ways:
- Localization is dynamic, the localization occurring only when assignment actually occurs in execution. This permits access to the global value of a name which is later localized, as in n←n .
- The symbol
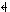 is used to denote assignment that does not
actuate localization.
is used to denote assignment that does not
actuate localization.
Although we had the means to represent an array of names by a character array, it did not occur to us to allow assignment of parts of a result to each ot a collection of names. In more recent modelling of the execution process [12], it became evident that the name n in the expression n←3×m was not evaluated before being “transferred to the execution stack”, but that parentheses could be used to force such evaluation, as in the following example:
n←'t' (n)←3 t 3
In the dictionary this notion is adopted in a manner that also
exploits the use of arrays of boxed names.
References
| 1. | Iverson, K.E., A Programming Language, Wiley, New York, 1962. | |
| 2. | Falkoff, A.D. and K.E. Iverson, APL\360 User’s Manual, IBM Corporation, August 1968. | |
| 3. | Falkoff, A.D. and K.E. Iverson, APLSV User’s Manual, IBM Corporation, 1973. | |
| 4. | Falkoff, A.D. and K.E. Iverson, The Design of APL, A Source Book in APL, APL Press, 1981. | |
| 5. | Falkoff, A.D. and K.E. Iverson, The Evolution of APL, SIGPLAN Notices 13, ACM, August 1978. | |
| 6. | McDonnell, E.E., The Story of ○ , APL Quote-Quad, Vol. 8. No. 2, ACM, SIGPLAN Technical Committee on APL (STAPL), December, 1977, pages 48-54. | |
| 7. | Iverson. K.E., Operators and Functions, IBM Research Report RC 7091, 1978. | |
| 8. | Bernecky, R.B., and K.E. Iverson, Operators and Enclosed Arrays, 1980 APL User’s Meeting, I.P. Sharp Associates. | |
| 9. | Iverson. K.E., Rationalized APL, I.P. Sharp Associates, April 1983. | |
| 10. | Iverson. K.E., A Dictionary of APL, I.P. Sharp Associates, July 1986. | |
| 11. | Iverson, K.E., APL Syntax and Semantics, APL83 Conference Proceedings. | |
| 12. | Iverson, K.E., and A.T. Whitney, Practical Uses of a Model of APL, APL Quote Quad Vol 13, No. 1, 1982. | |
| 13. | Hodgkinson, R., APL Procedures (User-Defined Operators, Functions, and Token Strings), APL86 Conference Proceedings. | |
| 14. | Iverson, K.E., A Dictionary of APL, APL Quote-Quad. (To appear). | |
| 15. | SHARP APL/UX User’s Guide, I.P. Sharp Associates. (To appear). | |
| 16. | Tuttle, J.K., Designing An APL Type Font, APL81 Conference Proceedings. | |
| 17. | Orth. D.L., Calculus in a New Key, APL Press, 1976. | |
| 18. | Iverson. K.E., Elementary Analysis, APL Press, 1976. |
Appendix A. SHARP APL/PC Main Keyboard
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
Appendix B. APL Alphabet and ASCII Transliteration
|
|
The ASCII [5] transliteration scheme in the last column is based upon similarity, English-Greek correspondences, and variants, denoted by an extra delimiter (@) and varying by rotation about a horizontal or vertical axis. Each transliteration begins with a delimeter and ends with a space.
Table 1
Errata
| • | In the Introduction, it should say “The Evolution of APL” instead of “the Evolution of APL”. | |
| • | In Section B, in the second paragraph, it should say “lower- and upper-case” instead of “lower and upper-case”. | |
| • | In Section C, the words and associated functions have several problems. First, the function g requires index origin 1 to work, but the example in Section E implies that the index origin is 0. Moreover, numeric vector constants are not supported, and the treatment of the period is problematic (e.g. plus.times is incorrectly considered to be a single word). | |
| • | In Section D, the first displayed example from the dictionary should end with ⊢ ⍴r instead of qltack ⍴r . | |
| • | In Section D, the expressions for computing the coefficients c of a polynomial with roots r should use -r instead of r in the inner products; that is, (-r)×.*t instead of r×.*t . | |
| • | In Section E, in the second paragraph, the reversal example is missing a right parenthesis. | |
| • | Reference 4, The Design of APL, first appeared in the IBM Journal of Research and Development, Volume 17, Number 4, July 1973. | |
| • | References 13 and 14 should end with “(To appear.)” instead of “(To appear).”. | |
| • |
In Appendix B, the ASCII transliterations for ←
and 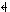 are both @<- .
The transliteration for the latter should be @<-| . are both @<- .
The transliteration for the latter should be @<-| .
|
Originally appeared in the APL87 Conference Proceedings, APL Quote-Quad, Volume 17, Number 4, 1987-05.
| created: | 2009-03-27 09:50 |
| updated: | 2013-09-29 23:00 |