28. Odometer

{⍵⊤⍤1 0⍳×/⍵}

The odometer function of a list of non-negative integers x counts from 0×x to x-1 . For example, the odometer of x←4 2 3 is:

0 0 0
0 0 1
0 0 2
0 1 0
0 1 1
0 1 2
1 0 0
1 0 1
1 0 2
1 1 0
1 1 1
1 1 2
2 0 0
2 0 1
2 0 2
2 1 0
2 1 1
2 1 2
3 0 0
3 0 1
3 0 2
3 1 0
3 1 1
3 1 2

Odometer can be computed in a variety of ways.

Base Representation

The odometer is the base x representation of ⍳×/x . Thus:

   odometer←{⍵⊤⍤1 0⍳×/⍵}

Cartesian Product

The odometer is the mixed ravelled cartesian product of ⍳0⊃x , ⍳1⊃x , ⍳2⊃x , etc.

   ⍳¨ x
┌───────┬───┬─────┐
│0 1 2 3│0 1│0 1 2│
└───────┴───┴─────┘
   ∘.,/ ⍳¨ x
┌───────────────────┐
│┌─────┬─────┬─────┐│
││0 0 0│0 0 1│0 0 2││
│├─────┼─────┼─────┤│
││0 1 0│0 1 1│0 1 2││
│└─────┴─────┴─────┘│
│┌─────┬─────┬─────┐│
││1 0 0│1 0 1│1 0 2││
│├─────┼─────┼─────┤│
││1 1 0│1 1 1│1 1 2││
│└─────┴─────┴─────┘│
│┌─────┬─────┬─────┐│
││2 0 0│2 0 1│2 0 2││
│├─────┼─────┼─────┤│
││2 1 0│2 1 1│2 1 2││
│└─────┴─────┴─────┘│
│┌─────┬─────┬─────┐│
││3 0 0│3 0 1│3 0 2││
│├─────┼─────┼─────┤│
││3 1 0│3 1 1│3 1 2││
│└─────┴─────┴─────┘│
└───────────────────┘
      ↑ , ⊃∘.,/ ⍳¨ x
0 0 0
0 0 1
0 0 2
0 1 0
0 1 1
0 1 2
1 0 0
...

   odometer1←{↑,⊃∘.,/⍳¨⍵}

Copy and Reshape

   ⍳¨ x
┌───────┬───┬─────┐
│0 1 2 3│0 1│0 1 2│
└───────┴───┴─────┘

   ⌽×\⌽1↓x,1
6 3 1
   ×/ x
24

   6 3 1 /¨ ⍳¨ x
┌───────────────────────────────────────────────┬
│0 0 0 0 0 0 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3│...
└───────────────────────────────────────────────┴
                                  ┬───────────┬─────┐
                               ...│0 0 0 1 1 1│0 1 2│
                                  ┴───────────┴─────┘
   ↑ 24 ⍴¨ 6 3 1 /¨ ⍳¨ x
0 0 0 0 0 0 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3
0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1
0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2
   ⍉ ↑ 24 ⍴¨ 6 3 1 /¨ ⍳¨ x
0 0 0
0 0 1
0 0 2
0 1 0
0 1 1
0 1 2
1 0 0
...

   odometer2←{⍉↑(×/⍵)⍴¨(⌽×\⌽1↓⍵,1)/¨⍳¨⍵}

Remainders of Quotients

   ×/ x
24
   ⌽×\⌽1↓x,1
6 3 1
   ⌊ (⍳24) ∘.÷ 6 3 1 
0 0  0
0 0  1
0 0  2
0 1  3
0 1  4
0 1  5
1 2  6
1 2  7
1 2  8
1 3  9
1 3 10
1 3 11
2 4 12
2 4 13
2 4 14
2 5 15
2 5 16
2 5 17
3 6 18
3 6 19
3 6 20
3 7 21
3 7 22
3 7 23
   4 2 3 |⍤1 ⌊ (⍳24) ∘.÷6 3 1 
0 0 0
0 0 1
0 0 2
0 1 0
0 1 1
0 1 2
1 0 0
...

   odometer3←{⍵|⍤1⌊(⍳×/⍵)∘.÷⌽×\⌽1↓⍵,1}

Counting in Base x

   successor←{⍺{(⍺|⍵)+1↓(⍺=⍵),0}⍣≡⍵+(-≢⍵)↑1}
         
   x successor 0 0 0
0 0 1
   x successor 0 0 1
0 0 2
   x successor 0 0 2
0 1 0
   x successor 0 1 0
0 1 1
   x {⍺ successor⍣⍵⊢0×⍺}⍤1 0 ⍳7
0 0 0
0 0 1
0 0 2
0 1 0
0 1 1
0 1 2
1 0 0

   odometer4←{⍵{⍺ successor⍣⍵⊢0×⍺}⍤1 0⍳×/⍵}

If the power operator were extended to accept non-scalar “exponents” (right operand), then the function can be simplified to:

   odometer4a←{⍵ successor⍣(⍳×/⍵)⊢0×⍵}

Some Applications of Odometer

The function pco from the D-Function website [89] computes the factorization of n as a 2-row matrix of the primes and the corresponding exponents. Whence all the divisors of n obtain as follows:

   2 pco 160
2 5
5 1

   divisors←{p e←↓2 pco ⍵ ⋄ p ×.*⍤1 odometer 1+e}

   divisors 160
1 5 2 10 4 20 8 40 16 80 32 160

There is a simple relationship between odometer on n-⍳n and the set of all permutations of ⍳n . See the Permutation Index chapter.

From http://xkcd.com/287

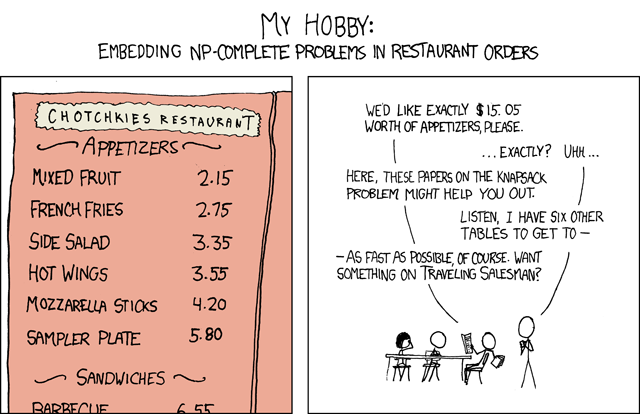
   a← 215 275 335 355 420 580
   n← 1 + ⌊ 1505 ÷ a
   n
8 6 5 5 4 3

   ⊢ s← (1505 = t +.× a) ⌿ t← odometer n
1 0 0 2 0 1
7 0 0 0 0 0
   s +.× a
1505 1505

That is, $15.05 worth of appetizers obtains by 1 mixed fruit, 2 hot wings, and 1 sampler plate, or by 7 mixed fruits.

Appeared in J in [90].