45. Euler’s Identity

Euler’s identity 0 = 1 + * ○ 0j1 is the most beautiful equation in mathematics, relating in one short phrase the fundamental quantities 0, 1, e, π, and 0j1 and the basic operations plus, times, and exponentiation. It is a particular case of Euler’s formula (*0j1×⍵) = (cos ⍵) + 0j1×(sin ⍵) Herewith a proof of Euler’s formula and Euler’s identity. *0j1×⍵ (!⍳∞) ÷⍨ e← ∞ ⍴ 1 0j1 ¯1 0j¯1 cos ⍵ (!⍳∞) ÷⍨ c← ∞ ⍴ 1 0 ¯1 0 sin ⍵ (!⍳∞) ÷⍨ s← ∞ ⍴ 0 1 0 ¯1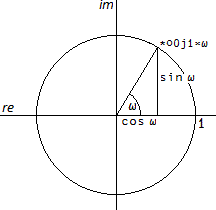

The three previous lines list three functions and their Taylor series coefficients. ∞ denotes infinity and is not (yet) implemented in APL [123, 124a]. For terms 0 2 4 6 8 … e is the same as for c , and for terms 1 3 5 7 … e is the same as for 0j1×s :

   e ⍪ c ⍪ ⍉⍪ 0j1×s
1 0j1  ¯1 0j¯1  1 0j1  ¯1 0j¯1  1 0j1
1   0  ¯1    0  1   0  ¯1    0  1   0 …
0 0j1   0 0j¯1  0 0j1   0 0j¯1  0 0j1

   e ⍪ ⍉⍪ c + 0j1×s
1 0j1  ¯1 0j¯1  1 0j1  ¯1 0j¯1  1 0j1 …
1 0j1  ¯1 0j¯1  1 0j1  ¯1 0j¯1  1 0j1

   e = c + 0j1×s
1 1 1 1 1 1 1 1 1 1 …

Since the series are absolutely convergent, it follows that

   (*0j1×⍵) = (cos ⍵) + 0j1×(sin ⍵)

It is not too far a leap to plug in an extremal value of the functions:

   cos ○1
¯1
   sin ○1
1.22461e¯16
   (cos ○1) + 0j1×(sin ○1)
¯1j1.22465e¯16

   (*0j1×○1) = (cos ○1) + 0j1×(sin ○1)
1

   1 + * ○ 0j1
0

I used to think math was no fun,
’Cause I couldn’t see how it was done.
    Now Euler’s my hero,
    For I now see why 0
Equals e to the π i plus 1.

e raised to the π times i,
And plus 1 leaves you nought but a sigh,
    This fact amazed Euler,
    That genius toiler,
And still gives us pause, bye the bye.

              — Anon y Mous

Appeared in J in [125].