

By relieving the brain of all unnecesary work, a good notation sets it free to concentrate on more advanced problems, and in effect increases the mental power of the race.
A. N. Whitehead
Some symbols, likethat were used originally for only positive integral values of n stimulated intellectual experimentation when n is fractional, negative, or complex, which led to vital extensions of ideas.
F. Cajori
Mathematical notation, like language, has grown up without much looking to, at the dictates of convenience and with the sanction of the majority.
A. de Morgan
The foregoing quotations assert both the power and the muddle of mathematical notation. They may be found in the concluding section of Volume II of Cajori, A History of Mathematical Notations [1]. Cajori also says: "In the light of the teaching of history it is clear that new forces must be brought into action in order to safeguard the future against the play of blind chance. The drift and muddle of the past is intolerable. We believe that this new agency will be organization and co-operation."
Writing in the 1920s, Cajori could not have foreseen the potential impact of the computer, and of the programming languages that have developed to apply it to mathematical problems.
For practical reasons, programming languages have largely adopted a standard alphabet (or character set, known as ASCII), unambiguous use of symbols (within any given language), and the discipline of a precisely defined grammar, or syntax. In spite of the wide use of programming languages in expressing and executing mathematical problems, the standardization and other notions from programming languages have had virtually no impact on the mathematical notation used in the exposition and teaching of mathematics.
It might be argued that mathematical notation (to be referred to as MN) is adequate as it is, and could not benefit from the infusion of ideas from programming languages. However, MN suffers an important defect: it is not executable on a computer, and cannot be used for rapid and accurate exploration of mathematical notions.
The remainder of this paper is a critique of MN, together with suggestions for improvement based on experience in the design of programming languages and in their use in the exposition of topics in mathematics.
In any criticism, it is important that suggestions for improvement come from a coherent and tested system, lest they be dismissed as disconnected, and possibly conflicting, proposals. For this reason I will base all suggestions on a single programming system. The system J is chosen for the following reasons:
The difficulty posed for the reader by the use of J (or any programming language) is that of understanding an unfamiliar notation. This will be eased by the fact that each expression can be executed, that its results are shown, and that most are accompanied by comments (in a distinct font).
We will follow the common convention of using italics in the names in MN, and a uniformly spaced font for expressions in programming languages. Any expression to be entered is shown indented, and its result is not indented.
Mathematics makes much use of relations such as less than (denoted by <), equals (=), and greater than (>); and the result of a relation is interpreted as true if the relation holds, and false otherwise.
Boole [8] denoted true by 1 and false by 0, and (by analogy with the behaviour of multiplication on these arguments) used the symbol for multiplication to denote logical and. By a looser analogy, he used + for logical or.
Later workers, wishing to use logical functions
together with arithmetic functions, introduced distinct symbols:
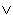 (from the Latin vel) for
or, and
(from the Latin vel) for
or, and 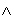 for and.
For the same reason, J (being confined to the ASCII alphabet)
uses +. for or, and *. for and. For
example:
for and.
For the same reason, J (being confined to the ASCII alphabet)
uses +. for or, and *. for and. For
example:
0 +. 0 The proposition p or q is false if both p and q are false
0
0 +. 1 The proposition p or q is true if p is false and q is true
1
1 +. 0
1
1 +. 1
1
1 *. 1 p and q is true if both p and q are true
1
MN uses the symbol = for a relation, but also uses it for assignment, as in the expression (Let) x=3. Again, to denote these two distinct notions without ambiguity, programming languages use distinct notation (that usually includes the symbol =), as in := (in ALGOL), and =: (in J). For example:
a=: 4 a is four
v=: 2 3 5 7 v is the vector of the first four primes
plus=: + plus is the function +
a * v a times v
8 12 20 28
v plus v v plus v
4 6 10 14
The use of executable notation for exploration is illustrated by the following passage from Chapter 2 of Exploring Math [6]:
It is commonly thought that math is about numbers. So it is, but numbers are not the only, nor even the most important, concern of math. It would be more accurate to say that math is concerned with relations, and with proofs of relations.
Although the first chapter dealt only with numbers, it should be clear that the interesting aspects were the relations between results. For example:
a=: i. 6 The first six non-negative integers
b=: ?.~ 6 The integers in random order
b
5 1 2 4 3 0
3*a
0 3 6 9 12 15
a+a+a
0 3 6 9 12 15
(3*a) = (a+a+a) The relation between multiplication and addition
1 1 1 1 1 1
a = b The lists a and b are not equal
0 1 1 0 0 0
sort=: /:~
sort b
0 1 2 3 4 5
sort a
0 1 2 3 4 5
(sort a)=(sort b) But are similar; one is a permutation of the other
1 1 1 1 1 1
We will further illustrate this matter of relations by examples that do not concern numbers. For example, the word 'POST' is said to be an anagram of the word 'SPOT' because the letters of 'SPOT' can be permuted to give the word 'POST'. Thus 'SPOT' and 'POST' are similar in the sense already defined for lists. The similarity of these words may be tested as follows:
w=: 'SPOT' x=: 'POST' sort w OPST sort x OPST (sort w)=(sort x) 1 1 1 1
Sorting w produces OPST. Is it an anagram? We will say that it is, although it is not an English word.
You could (and should) attempt to write down all distinct anagrams of 'SPOT', finding a surprising number of English words among them. However, this might be rather difficult to do; in a long list of words it is easy to overlook repetitions, and you may not even know how many anagrams to expect all together.
We will now use the anagram function A. for this purpose. Its left argument chooses one of many permutations to apply to the list right argument. Thus:
w
SPOT
8 A. w
POST
12 A. 8 A. w The permutation 12 A. is the inverse of 8 A.
SPOT
0 1 2 3 4 5 6 7 8 A. w
SPOT
SPTO
SOPT
SOTP
STPO
STOP
PSOT
PSTO
POST
30 A. w
|index error
| 30 A.w
The last result shows that there is a limit to the valid left argument; properly so, since there is a limit to the number of different permutations of a list. But how many are there? In the case of a two-item list 'AB' there are clearly only two possibilities, the identity permutation that leaves the list unchanged, and the one that gives 'BA'. Thus:
0 1 A. 'AB' AB BA
Write down all permutations of the list 'ABC' to convince yourself that there are six possible permutations. Thus:
(i. 6) A. 'ABC' ABC ACB BAC BCA CAB CBA
In discussing number systems
it is common to use a phrase such as "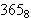 is 555" to
indicate that the base-8 representation of the number of days
in a year is 555. This is predicated on the fact that the 365
is "obviously" expressed in decimal. How, then, do we
indicate the inverse case? what would the result of
is 555" to
indicate that the base-8 representation of the number of days
in a year is 555. This is predicated on the fact that the 365
is "obviously" expressed in decimal. How, then, do we
indicate the inverse case? what would the result of 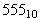 be?
And what is one to make of the expression "
be?
And what is one to make of the expression "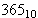 is 365"?
is 365"?
These matters may be clarified by the use of lists; a number is represented by a list of digits. For example:
d=: 3 6 5
w=: 100 10 1 Weights for decimal (base 10)
d * w
300 60 5
It
remains to apply addition over the list d*w, a matter
expressed in MN by 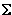 . The applications of other functions
over a list are denoted similarly, using
. The applications of other functions
over a list are denoted similarly, using  for product,
for product, 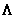 for and,
and
for and,
and 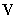 for or. The general notion is simply the modification
of a function by an operator in the sense introduced by
Heaviside [9].
for or. The general notion is simply the modification
of a function by an operator in the sense introduced by
Heaviside [9].
As used by Heaviside in the treatment of differential equations, the notion seems too difficult for use at an elementary level. However, the obvious analogy between a function in math, and a verb in English, leads to the notion of a Heaviside operator as the analog of an adverb, something that modifies a verb to produce a different, though related, verb. Not only is the term adverb more suggestive than operator, but it avoids conflict with its use in MN as a synonym for function. Finally:
+/d*w Sum over product of d and w. The / is an adverb that modifies +
365
The parallel with the adverb is apropos: in English (and other natural languages), the use of m verbs together with n adverbs permits the prescription of m times n related verbs. The adverb is equally prolific in a mathematical context. For example:
+/ d Sum over (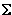 )
)
*/ d Product over ( )
)
*./ d < w And over (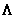 )
)
+./ d < w Or over (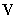 )
)
>./ d Max (greater of) over
<./ d Min (lesser of) over
In English, a
conjunction (such as the copulative conjunction and in
the phrase run and hide) can apply to two verbs to produce
a related verb. Analogously, an operator in math may apply to
two functions (as in the composition 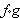 , and in convolution),
or to a verb and a noun, as in Currying
, and in convolution),
or to a verb and a noun, as in Currying or bonding.
For example:
or bonding.
For example:
pof=: */ @ ! Product over atop factorial
pof d=: 3 6 5 (!3)*(!6)*(!5)
518400
cube=: ^&3 Power with 3
cube d
27 216 125
^.
d Natural logarithm
1.09861 1.79176 1.60944
10&^. d Base 10 logarithm
0.4771213 0.7781513 0.69897
Conjunctions, like adverbs, are very prolific, providing simple expressions for a host of special notations in MN. For example, falling and rising factorial functions (denoted in Concrete Mathematics [11] by underscored and overscored superscripts) may be expressed in the form of the product x(x+s)(x+2s)(x+3s) for s=-1 and s=1, respectively. Since the case s=0 is equivalent to the power function, the factorial functions are denoted by ^!._1 and ^!.1, using the conjunction !. (called fit). For example:
x=: 5
m=: 4
x ^!._1 m Falling factorial
120
x*(x-1)*(x-2)*(x-3)
120
*/x,(x-1),(x-2),(x-3)
120
x - i. m
5 4 3 2
*/ x - i. m
120
x ^!.0 m Power
625
rf=: ^!.1 Rising factorial
x rf m
1680
 Named for Haskell Curry, who introduced
the notion in discussing Combinators [10].
Named for Haskell Curry, who introduced
the notion in discussing Combinators [10].
In chemistry, the number of atoms that will bind with a given atom is called its valence. Adopting this notion, we will say that a function such as addition (that applies to two arguments) has valence 2, that the sum function +/ derived from it has valence 1, and that (because it may be used with either one argument or two), the function denoted by - is ambivalent. The effective valence of - is determined by context. For example:
d=: 3 6 5 5-d 2 _1 0 -d _3 _6 _5
Not only does ambivalence obviate a further symbol for negation, but it provides a useful mnemonic: -d is equivalent to 0-d.
This ambivalence of - goes unremarked in MN. Moreover, the notion remains unexploited; it could be used to good effect for a wide class of dyadic functions:
3 % 5 Division
0.6
% 5 Reciprocal (1%5)
0.2
3 ^ 5 Power
243
^ 5 Exponential (e^5, where e is Euler's number 2.71828...)
148.413
3 ! 5 Binomial coefficient ((!5) % (!3) * (!5-3))
10
!5 Factorial
120
3 < d
0 1 1
< d
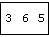
3 > d
0 0 0
> < d
3 6 5
The final examples illustrate how the mnemonic may be visual rather than relational: < packs its argument into a box, and > opens it.
In J, all functions are ambivalent, including not only primitive functions but those derived from them by the use of operators. For example:
*/ d Times over
90
1 2 3 4 */ 1 2 3 4 Times table
1 2 3 4
2 4 6 8
3 6 9 12
4 8 12 16
pt=: 0 1 2 3 4 !/ 0 1 2 3 4
pt Pascal's Triangle (with meaningful zeros)
1 1 1 1 1
0 1 2 3 4
0 0 1 3 6
0 0 0 1 4
0 0 0 0 1
X=: +/ . * Matrix product produced by the dot operator
pt X pt
1 2 4 8 16
0 1 4 12 32
0 0 1 6 24
0 0 0 1 8
0 0 0 0 1
X pt The monadic case is the permanent
1 (-/ . * is the determinant)
Altogether, ambivalence provides an enormous, unobtrusive, and mnemonic economy of symbols.
In MN, a product may be written in
the form 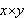 (or, perhaps x*y), but can also
be written as xy or x y, omitting the symbol for
multiplication. The brevity achieved by such elision is attractive,
and is widely used.
(or, perhaps x*y), but can also
be written as xy or x y, omitting the symbol for
multiplication. The brevity achieved by such elision is attractive,
and is widely used.
Other function symbols are also elided, as
in 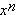 for power (the function being indicated only by the
raised position of the exponent n), and in MN or
M N for the matrix product (distinguished from the elided
product xy only by the capital letters that must be used
to denote the arguments).
for power (the function being indicated only by the
raised position of the exponent n), and in MN or
M N for the matrix product (distinguished from the elided
product xy only by the capital letters that must be used
to denote the arguments).
The consequences of such elision are often overlooked:
Programming languages avoid such issues very simply: every function must have a symbol, and it must be used.
Although MN deals with scalars, vectors,
matrices, and higher-rank arrays, it fails to provide a complete
and uniform system, particularly in the case of empty arrays.
For example, the definition of the falling factorial in Concrete
Mathematics [11] reads as x(x-1)...(x-m+1),
together with an indication that m factors are to be taken.
This pattern provides clear instructions for m down to
1, but the case of 0 requires the following note: "When m
= 0, we have 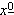 = 1, because a product of no factors
is conventionally [italics added] taken to be 1 (just as
a sum of no terms is conventionally 0)."
= 1, because a product of no factors
is conventionally [italics added] taken to be 1 (just as
a sum of no terms is conventionally 0)."
A vector may be partitioned by taking and dropping k items from it, and (because addition is associative) the sum of the sums of the parts will equal the sum over the original vector. For example:
x=: 2 3 5 7 11
k=: 3
a=: k {. x k take from x
a
2 3 5
b=: k }. x k drop from x
b
7 11
f=: +
f/a
10
f/b
18
(f/a) f (f/b)
28
f/x
28
The link function (;) boxes its arguments and then catenates them; it can be used to display related results compactly for comparison. For example:
k=: 3
a=: k {. x
b=: k }. x
b ; |. b
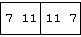
a ; b ; (f/a) ; (f/b) ; ((f/a)f(f/b)) ; (f/x)
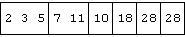
The case k=: 0 selects an empty vector, and the sum over it ("obviously" zero) satisfies the required identity:
k=: 0
a=: k {. x
b=: k }. x
a ; b ; (f/a) ; (f/b) ; ((f/a)f(f/b)) ; (f/x)
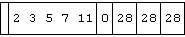
Because multiplication is also associative, it satisfies a similar identity:
a ; b ; (*/a) ; (*/b) ; ((*/a)*(*/b)) ; (*/x)
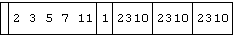
Again the function over the empty vector satisfies the identity, but its value may no longer seem so obvious. The case of the minimum function (also associative) may be even more surprising:
f=: <.
a ; b ; (f/a) ; (f/b) ; ((f/a)f(f/b)) ; (f/x)
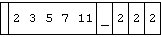
Since 0+x equals x for any value of x, zero is said to be the identity element or neutral of the function +. Similarly, 1 is the identity element of *, and it is clear that the result of f/ on an empty vector must be the identity element of f if the identity over partitions is to hold.
Why the result _ (infinity) for the case of minimum? Because that is its identity element.
These results for empty vectors are of practical significance, and arise frequently. Consider, for example, the following calculation of the falling factorial:
x=: 5
m=: 4
i. m The first m non-negative integers
0 1 2 3
x - i. m The factors of the falling factorial
5 4 3 2
*/ x - i. m The falling factorial
120
*/ x - i. 0 This correct result is the product over an empty vector
1
Matrices, matrix product, and matrix inverse are commonly introduced at high-school level and used in the treatment of linear equations. However, we fail to exploit them in many elementary and interesting ways. This failure rests partly on the propensity to present significant matrices in truncated form by suppressing (presumably for readability) zero elements.
For example, the table of binomial coefficients introduced in Section E appears as:
pt=: 0 1 2 3 4 !/ 0 1 2 3 4 pt 1 1 1 1 1 0 1 2 3 4 0 0 1 3 6 0 0 0 1 4 0 0 0 0 1
but is commonly presented as a triangle (Pascal's triangle) by suppressing the zeros in the lower left. These zeros are meaningful results. For example, the number of ways of choosing 4 elements from a list of three items (4!3) is 0.
Although Pascal's triangle cannot be treated as a matrix, the table pt can. For example, its inverse (produced by the function %.) is the table of alternating binomial coefficients:
abc=: %. pt abc 1 _1 1 _1 1 0 1 _2 3 _4 0 0 1 _3 6 0 0 0 1 _4 0 0 0 0 1
Moreover, the sums of the columns of these matrices produce interesting results:
+/ pt 1 2 4 8 16 +/ abc 1 0 0 0 0
The "expansion" of the coefficients of a polynomial may be expressed simply and clearly as a matrix product of the matrix of binomial coefficients and the coefficients. For example:
X=: +/ . * Matrix product
x=: 0 1 2 3 4 5 6 Argument of polynomial
c=: 3 1 4 2 1
c p. 2 Polynomial (ascending powers)
53
c p. x
3 11 53 177 455 983 1881
d=: pt X c Expanded coefficients
d
11 19 16 6 1
d p. x Equivalent to c p. (x+1)
11 53 177 455 983 1881 3293
c p. x+1
11 53 177 455 983 1881 3293
The following is from Chapter 6 of Exploring Math [6]:
Special terminology used in various branches of knowledge often imposes a serious burden on a beginner. It may sometimes be safely dismissed as pretentious and no better than familiar terms, but serious treatment of a topic may well require finer distinctions than those provided by familiar language. For example, the familiar average may sometimes be substituted for mean as defined in math and statistics. However, mean refers not only to average (the arithmetic mean), but also to various ways of characterizing a collection by a single number, including the geometric mean, harmonic mean, and common mean.
Similarly, the grammatical terms adopted in J (from English) may seem pretentious to anyone familiar with corresponding terms in math, but they make possible significant distinctions that are not easily made in MN. We illustrate this by a few sentences and the classification of items from them in both J and MN:
with=: & cube=: ^ with 3 commute=: ~ into=: % commute pi=: 7 into 22 2 into cube a=: i. 6
J MN Noun 22 Constant Pronoun pi Variable Verb or Function % Function or Operator Proverb cube Adverb or Operator ~ Operator Pro-adverb commute Conjunction or Operator & Operator Pro-conjunctionx with List or Vector a Vector Table or Matrix a*/a Matrix Report or Array a +/ a */ a Array
In the foregoing, MN makes the same distinction made by noun and pronoun in J, but uses the terms constant and variable. The term variable may prove somewhat misleading, particularly when used for a pronoun such as pi (for the ratio of the circumference to the diameter of a circle), which is not expected to vary. The following sentences may be used to clarify the choice of the word variable:
sqr=: *: The square function in J
(sqr 0)=(0+0)
(sqr 2)=(2+2)
(sqr 0)=(0*0)
(sqr 2)=(2*2)
(sqr 3)=(3*3)
Each of these sentences express a "true" relation in the sense that each comparison yields 1. However, the first pair are true only for the specific arguments 0 and 2, and for no other. The last three suggest (correctly) that the indicated relation remains true for any argument, or, as we say, the argument is allowed to vary. This generality is commonly indicated by using a pronoun argument, or, as stated in MN, a variable:
(sqr x)=(x*x)
In MN, the term operator (or functional) is used for both of the cases distinguished in J by adverb and conjunction. Moreover, in MN the term operator is also commonly used to refer to functions.
The terms list, table, and report are used in J with meanings familiar to anyone, whereas the corresponding terms vector, matrix, and array might be known only to specialists. The familiar use of vector is as a carrier, as in disease vector. It might be thought that a vector "carries" its items, but the actual etymology of the term in math is quite different, although not as bizarre as that of matrix.
New terminology should be approached by using dictionaries to learn the etymology of terms, both old and new. For example, a verb is defined as a word that (amongst other things) expresses an action; the corresponding word function comes from a root meaning "to perform".
Attention to etymology is also rewarding in every-day work. For example, the meaning of atom appears clearly in its derivation (a[not] + tem[cut]) as something that could not be cut.
The American Heritage Dictionary [12] presents etymology in a particularly revealing manner: all words derived from a given root are listed together in an appendix. This highlights surprising and insightful relations, such as that between tree and true. As a further example, the root tem that occurs in atom also occurs in anatomy, microtome, and tome. Incidentally, tome does not necessarily mean a big book, but rather one of the volumes "cut" from a book, such as the 24 tomes of the original Oxford English Dictionary.
Lewis Thomas, a noted bio-chemist, explored the pleasure and profit of etymology in his delightful book et cetera, et cetera. [13]. It is well worth reading.
The discussion thus far has proceeded largely by taking phrases in MN and showing how they might be re-expressed in J. Moreover, the examples used have all been elementary, being restricted to topics treated in high-school math, and to an elementary subset of the facilities available in J.
The reader may gain a deeper appreciation of the weaknesses of MN by the converse: take statements from some of the J publications listed in the references, and attempt to re-express them in MN, avoiding as much as possible the use of English phrases to paper over any deficiencies. In particular, it will be helpful to compare the treatment in Concrete Math Companion [14] with the conventional treatment of the same topics in Concrete Mathematics [11].
We will illustrate the process by a few examples, showing the complete results of all J expressions used so that the reader may see clearly what is to be produced, even though all details of the J expressions may not be clear. For example:
x=: 2 3 5 7 11
+/x Sum
28
-/x Alternating sum
8
These may be re-expressed as 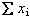 and
and
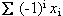 , respectively. In general, the use
of -/ and the correspondingly modified matrix product -/ . *
obviates the use of the phrase
, respectively. In general, the use
of -/ and the correspondingly modified matrix product -/ . *
obviates the use of the phrase 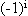 .
.
The prefix scan adverb \ leads to a more interesting case:
<\x Box each prefix of x
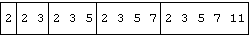
st=: +/\x Subtotals (sum each prefix)
st
2 5 10 17 28
In
MN it is usual to express the element  by using
by using  with upper and lower
limits, but it should be noted that this specifies the complete
result st only implicitly by specifying a typical element.
with upper and lower
limits, but it should be noted that this specifies the complete
result st only implicitly by specifying a typical element.
As shown in Section H, multiplication of a vector of polynomial coefficients by the binomial coefficients table pt (to be called bc here) served to produce the expanded coefficients. The conjunction & (with) may therefore be used to produce an expansion function exp as follows:
X=: +/ . *
bc=: 0 1 2 3 4 !/ 0 1 2 3 4
bc
1 1 1 1 1
0 1 2 3 4
0 0 1 3 6
0 0 0 1 4
0 0 0 0 1
exp=: bc&X
c=: 3 1 4 2 1
x=: 0 1 2 3 4 5 6
c p. x
3 11 53 177 455 983 1881
exp c
11 19 16 6 1
(exp c) p. x
11 53 177 455 983 1881 3293
c p. x+1
11 53 177 455 983 1881 3293
exp exp c
53 73 40 10 1
(exp exp c) p. x
53 177 455 983 1881 3293 5387
c p. x+2
53 177 455 983 1881 3293 5387
exp ^: 3 c Apply exp three times
177 187 76 14 1
(exp ^: 3 c) p. x
177 455 983 1881 3293 5387 8355
c p. x+3
177 455 983 1881 3293 5387 8355
The expansion function may also be applied to the table bc itself, to produce successive matrix products of the binomial coefficients table:
exp bc 1 2 4 8 16 0 1 4 12 32 0 0 1 6 24 0 0 0 1 8 0 0 0 0 1
<"2 exp^:0 1 2 3 bc
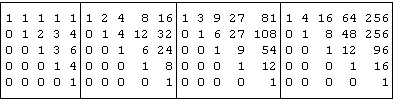
These tables show a pattern, and if we could find some alternative expression for each of them we would, in effect, express a host of identities concerning the binomial coefficients. If we divide each table by bc itself (using ordinary element-by-element division) we do obtain a simple pattern of powers of the "order" of each table:
<"2 (exp^:0 1 2 3 bc) %"2 bc
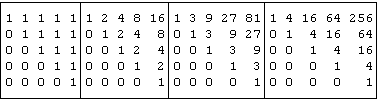
May we expect programming languages to have a salutary effect on MN? Not if it continues as de Morgan says "at the dictates of convenience". In particular, any ideas from programming languages would then be adopted piecemeal, further muddying the waters.
Perhaps, on the other hand, the practical advantages of executable notation, and the pedagogical advantages of a strict and simple grammar, will lead to the adoption of more fundamental and systematic change.