Operators and Functions
Kenneth E. Iverson
APL Design Group, Research Division, Yorktown Heights
Abstract
This paper treats the syntax of operators in APL, presents definitions of a number of new operators and functions, and provides examples of their use.
This paper presents some of the operators and functions which I have found useful in treatments of topics in mathematics and in data processing. Readers are assumed to be familiar with APL as defined in Reference [1]. I am indebted to a number of my colleagues for useful discussions and suggestions, particularly to A.D. Falkoff and D.L. Orth. I am also indebted to Michael Halpern for discussions leading to the formulation of the axis operator.
To allow functions to be defined as conveniently
as variables we will permit the use of the assignment
arrow  as follows:
a name followed
by
as follows:
a name followed
by  followed
by an expression which produces a function,
assigns the name to the function,
Thus f
followed
by an expression which produces a function,
assigns the name to the function,
Thus f +.×
and g
+.×
and g +
and h
+
and h g are valid expressions.
g are valid expressions.
Operators may take numeric, character, and even operator, arguments as well as functions. For example, the slash (/) applied to a dyadic function (as in +/) produces the monadic reduction function, and applied to a Boolean vector (as in u/) produces the monadic selection function called compression. Numeric operator arguments introduce the possibility of two juxtaposed vector constants in a valid expression. The ambiguity inherent in such juxtaposition must be resolved by the use of parentheses.
Zero-origin indexing will be used throughout this paper.
1. Syntax and Order of Execution
A function produced by an operator is called a derived function. Defined and derived functions behave like primitive functions in that they may serve as arguments to operators and may be divalent. Although derived functions may be divalent, the operators themselves are not. For example, reduction (/) and scan (\) are monadic and the dot (in inner and outer product) is dyadic. The jot (∘) as used in the outer product (∘.×) produces, in effect, a special “monadic case” of a dyadic operator. It will be used extensively in this manner in the definition of new operators.Since a monadic function applies to the argument to its right, and a monadic operator applies to the argument to its left, operators and functions behave in a syntactic sense as mirror images. This behavior will be carried through in the rules laid down for the order of execution.
The order of execution of functions in an unparenthesized expression is governed by a single rule: the right argument of any function (monadic or dyadic) is the result of the entire expression to the right of it. An operator (monadic or dyadic) applies in a similar manner to the left except that its left argument is the result of the longest possible operator sequence on its left. An operator sequence is a portion of an expression consisting of a non-operator followed by a sequence consisting of monadic operators or of dyadic operators each followed by one non-operator. The non-operators may themselves result from parenthesized expressions. Finally, operators enjoy precedence over functions in the sequence of execution, and obey parentheses in the usual manner.
Composite symbols formed from the dieresis (¨) and the overbar (¯) will be reserved exclusively for operators, but operator symbols will not be limited to this class. The symbols _ and ¯ denote infinity and negative infinity, respectively.
2. Power and Identity Operators
The power operator, denoted by ⍣ , applies to a monadic function left argument f and an integer right argument k to produce the kth power of f in the following sense: f⍣k ↔ f f⍣k-1 , and f⍣1 ↔ f . In particular, f⍣0 is the identity function and f⍣¯1 is the inverse of f . Moreover, f⍣_ denotes the limit of f , that is, the limiting function f⍣n for n large. Similarly, f⍣¯ denotes the limit of the inverse of f .The expression f⍣∘ yields the identity function of a dyadic function f , defined to be the function g with the following properties: a g 1 ↔ a , and a g 0 yields the identity element of f . Thus × is the identity function of + and * is the identity function of × , properties which account for the utility of expressions of the form b+.×l and b×.*l in applying the functions + and × over subsets of the elements of a vector b specified by the Boolean array l .
For example, if l←(k⍴2)⊤⍳2*k←⍴b , then b+.×l and b×.*l give sums and products over all subsets of b . Moreover, b⌊.(⌊⍣∘)l and b⌈.(⌈⍣∘)l give minima and maxima over all subsets of b . Finally, x∨.(∨⍣∘)l and x∧.(∧⍣∘)l clearly apply the functions ∨ and ∧ over all subsets of x , whereas the equivalent expressions x∨.∧l and x∧.≥l are not so obviously applications of ∨ and ∧ over subsets.
3. Commutator
The monadic operator ⍨ commutes the sense
of the arguments of a dyadic function f ,
that is,
4. Scalar Operators and the Identity Function
For each of the scalar dyadic primitive functions, we define an associated dyadic operator denoted by the symbol for the function overstruck with the overbar. The definition will be illustrated by the definition for + :
| (monadic) | f g y ↔ (f y) + (g y) g y ↔ (f y) + (g y) | |
| (dyadic) | x f g y ↔ (x f y) + (x g y) g y ↔ (x f y) + (x g y) |
The sum over the values produced
by the function f applied
to its entire domain will be denoted
by ∘ .
∘ .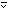 ∘ is 1 if and only if
there exists an element of its domain
for which p is true,
and the number of elements
in the set defined by p is given
by p
∘ is 1 if and only if
there exists an element of its domain
for which p is true,
and the number of elements
in the set defined by p is given
by p ∘ .
∘ .
If f is divalent,
the expression f ∘
applies to the monadic function denoted
by f ;
the dyadic form must be specified explicitly
in the manner presented in the following section.
∘
applies to the monadic function denoted
by f ;
the dyadic form must be specified explicitly
in the manner presented in the following section.
One of the arguments of a scalar operator
may be numeric,
in which case the following definitions
(shown for the specific scalar
function 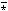 and the specific numeric quantity 2)
apply:
and the specific numeric quantity 2)
apply:
2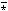 f y ↔ 2*f y
f
f y ↔ 2*f y
f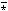 2 y ↔ (f y)*2
x 2
2 y ↔ (f y)*2
x 2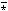 f y ↔ 2*x f y
x f
f y ↔ 2*x f y
x f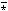 2 y ↔ (x f y)*2
2 y ↔ (x f y)*2
Certain of the scalar operators
are very useful in the treatment of sets.
If we consider the proposition
(i.e., a function whose result
is 0 or 1) p
which defines a set
(i.e., p x is 1 if x
belongs to the set and 0 if it does not),
then p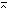 q defines the intersection
of the sets defined
by p and by q .
Similarly, p
q defines the intersection
of the sets defined
by p and by q .
Similarly, p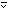 q
gives the union,
q
gives the union,
p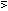 q
the ordinary difference,
and p
q
the ordinary difference,
and p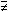 q the symmetric difference.
q the symmetric difference.
Use of the
form p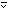 ∘
will be illustrated
by a proof of the fact that
the number of elements in the union of
sets p and q (that
is, p
∘
will be illustrated
by a proof of the fact that
the number of elements in the union of
sets p and q (that
is, p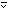 q
q ∘)
is equal to the sum of the numbers
in p and q ,
less the number in the
intersection p
∘)
is equal to the sum of the numbers
in p and q ,
less the number in the
intersection p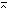 q .
For boolean arguments a and b ,
the expression a∨b is equivalent
to (a+b)-a∧b .
Consequently, p
q .
For boolean arguments a and b ,
the expression a∨b is equivalent
to (a+b)-a∧b .
Consequently, p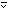 q ↔ (p
q ↔ (p q)
q)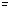 (p
(p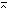 q) , and:
q) , and:
p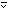 q
q ∘
(p
∘
(p q)
q)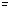 (p
(p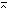 q)
q) ∘
(p
∘
(p q
q ∘)-(p
∘)-(p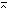 q
q ∘)
(p
∘)
(p ∘)+(q
∘)+(q ∘)-(p
∘)-(p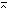 q
q ∘)
∘)
Further examples of the use of scalar operators will be found in the treatment of the derivative operator in Section 11.
5. Domain and Valence Operators
If f is a function,
then f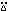 ∘ is a proposition of the same valence,
and with an unrestricted domain,
which defines the domain of f in the following sense:
∘ is a proposition of the same valence,
and with an unrestricted domain,
which defines the domain of f in the following sense:
| (monadic) | f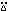 ∘ x is 1
if x is in the domain of f . ∘ x is 1
if x is in the domain of f . | ||
| (dyadic) | x f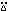 ∘ y is 1
if the pair x, y is in the domain of f . ∘ y is 1
if the pair x, y is in the domain of f . |
If f is a function
and p is a proposition
of the same valence,
then f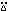 p is a function equivalent to f
but further restricted to the domain defined by p .
Formally:
p is a function equivalent to f
but further restricted to the domain defined by p .
Formally:
f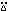 p
p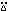 ∘ ↔ f
∘ ↔ f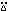 ∘
∘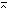 p
p
The valence of a function f
may be delimited by one of the
expressions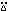 1
1 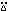 2 ,
2 ,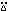 2
2 ∘ ,
∘ ,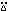 1
1 ∘
or f
∘
or f ∘ .
∘ .
6. Uniform Functions
A number of familiar monadic functions can be characterized by the rank of the argument or arguments for which they are defined, and by the ranks of the results they produce. For example:
| Expression | Rank | |||
| Monadic: | ||||
| |¯3 | 0 0 | |||
| +/1 2 3 4 5 | 0 1 | |||
| ⍳5 | 1 0 | |||
| ⌽ 1 2 3 4 5 | 1 1 | |||
| Determinant | 0 2 | |||
| Matrix inverse ( ⌹ ) | 2 2 | |||
| Dyadic: | ||||
| 3+4 | 0 0 0 | |||
| 2 2 2 ⊤ 6 | 1 1 0 | |||
| 3 ⌽ 1 2 3 4 5 | 1 0 1 | |||
| 2 1 4 ⌹ m | 1 1 2 |
In general, functions are defined to have an explicit rank, although degenerate cases of lower rank are sometimes permitted, as in reduction or reversal of a scalar, or as in ⌹ 1 2 3 . We will therefore speak of the rank of a function as a vector whose first element specifies the result rank and whose remaining element or elements specify the argument rank or ranks. There remain some open questions concerning the specification of the ranks of certain functions (such as ravel) which appear to be of unrestricted rank.
Arguments and results of fixed ranks may still vary in shape, and we now define a uniform function as one whose result shape depends only upon the argument shape. For example, reversal, reduction, and scan are uniform functions, but ⍳n is not. The importance of uniform functions is that their definition can be extended to arguments of higher rank in a systematic way, the argument being treated as an array of “subarrays” (along final axes which define the units of the function of appropriate rank), and the result is treated as the same array of subarrays of individual results. Non-uniform functions can be extended in a similar manner by employing the scalar representation function discussed in Section 10.
A uniform monadic function of rank rr,ar (result rank and argument rank) applies to an array x of rank ar or greater, to produce an overall result of rank ((-ar)↓⍴x),rr . The result can be perceived as follows: f is applied to each of the rank ar “units” of an “array of rank (-ar)↓⍴x” whose elements are these units, the rr coordinates of the individual results being placed last to produce the overall result of rank ((-ar)↓⍴x),rr .
7. Nuclear Axis Operators
The nuax operator (denoted by ⍤) applies to a function left argument and a variable right argument to specify the axes which define the nuclei to which the function is to apply. For example, if ⍴a is 3 4 3 5 5 and f is the determinant function (of rank 0 2), then f a yields a result of shape 3 4 3 , and f⍤0 2 a yields a result of shape 4 5 5 . The coax operator ⍥ is also provided; its argument specifies the axes complementary to the nuclear axes. For example, f⍥ 1 3 4 a is equivalent to f⍤ 0 2 a , whereas f⍥ 4 3 1 a has shape 5 5 4 .
It must be emphasized that if a function f has a result rank greater than zero, the corresponding axes occur as the final axes in the overall result, and that the axial operators do not specify the allocation of these “result” axes in the overall result. In this they differ from the use of brackets to specify axes, as in +\[3]a and ⌽[3] a , since the 3 in these cases specifies not only that the units be along axis 3 , but also that the vector results are to lie along the same axis. For example, if ⍴a is 2 3 4 5 , then ⍴+\[2]a is also 2 3 4 5 , but the result of plus scan over axis 2 as specified by the nuax operator has shape 2 3 5 4 .
The fact that the result axes occur last in the overall result is often convenient. For example, +/(,⍤i) a sums over the axes i of a .
For a dyadic left argument f, the right argument of the axis operator ⍤ has the form i,_,j , where i and j are vectors (of any length, including zero) specifying the units of the left and right arguments respectively (and where _ represents infinity). For example, ⌹⍤1 _ 1 3 applies ⌹ to vector left arguments along axis 1 and to matrix right arguments along axes 1 and 3 . Similarly, k⌽⍤ _3 a rotates the vectors along axis 3 of a by amounts specified by the scalars of k .
If the right argument of ⍤ requires the general form i,_,j , then any right argument k which does not include an infinity applies to specify axes of both the left and the right argument of the resulting derived function and is therefore equivalent to k,_,k . The argument _,k is, of course, equivalent to '',_,k and specifies scalar units in the left argument, and k,_ specifies scalar units on the right.
8. Composition and Duality
The dual operator, denoted by ⍢ , is a slight extension of the notion of dual functions implicit in deMorgan’s law ( ∨⍢~ ↔ ^ and ≠⍢~ ↔ =), the extension being to include a monadic left argument, as in ⌊⍢-x ↔ ⌈x . Composition, denoted by ¨ , is the familiar notion of the composition of two monadic functions ( f¨g x ↔ f g x) extended to the two cases of one dyadic argument, as well as to the case of character arguments which define a function in terms of the expression represented by one of the arguments.
Duality and simple composition. Composition and the dual operator applied to a divalent left argument and a monadic (or divalent) right argument yield parallel definitions of divalent derived functions as follows:
| Composition: | f¨g y ↔ f g y | |
| x f¨g y ↔ (g x) f (g y) | ||
| Dual: | f⍢g y ↔ (g⍣¯1) f (g y) | |
| x f⍢g y ↔ (g⍣¯1) (g x) f (g y) |
It should be noted that the extension of the dual to include the monadic definition makes the identities ⌈⍢- ↔ ⌊ and ⌊⍢- ↔ ⌈ hold for both the monadic case (floor and ceiling) and for the dyadic case (minimum and maximum). Moreover, for the dyadic case the exponential function yields the identities ×⍢* ↔ + and +⍢⍟ ↔ × , the latter of which provides the basis for the use of natural logarithms in multiplication, just as the identity +⍢(10¨⍟) ↔ x forms the basis for the use of base ten logarithms.
In the dyadic case of composition above, the first function f is dyadic and the second function g is monadic. This is the case that prevails when the functions have these valencies or are divalent. If either f is specifically monadic or g is specifically dyadic, we obtain another important case defined as follows:
x f¨g y ↔ f x g y
For divalent functions this form can be obtained by fixing the valence of one or both of the functions with the valence operator defined in Section 5. Frequently the valence becomes fixed by composition with a variable (as defined in the following subsection), as in the expression 2¨* .
The corresponding case for the dual operator ( f⍢dg) would lead to the definition f⍣¯1 f x dg y . It would therefore be vacuous (being equivalent to dg) and is consequently excluded.
The definition of the composition f¨g given above must be understood as referring to a single argument of rank appropriate to the function g . For example, if f is ⍉ and g is ⌹ , and ⍴a is 3 4 4 , then the units of g are 4 by 4 matrices, each of which is inverted and transposed to produce an overall result of shape 3 4 4 . Thus (assuming that ⌹ is of rank 2 2 , and extends to higher rank arrays in the normal manner) ⍉¨⌹a differs from the expression ⍉ ⌹ a since the latter would invert each of the three 4 by 4 matrices of a to produce a result of shape 3 4 4 which would then be transposed to produce a result of shape 4 4 3 .
Similar remarks apply to the dual operator,
and in general to all operators.
In other words, a derived function applies
as an indivisible whole to each
of the nuclei of its argument.
The dual operator is defined formally
in terms of composition as
follows:
f⍢g ↔ g⍣¯1¨(f¨g) .
Composition with one variable argument. The composition operator applied to a function f and a variable v produces a result of valence one less than the valence of f . Thus if f is dyadic, the result is monadic; if f is monadic, the result is a constant. For example:
| *¨.5 x | ↔ | x*.5 | ( *¨.5 is monadic) | ||
| *¨.5 | ↔ | *.5 | (A constant value) | ||
| 2¨* x | ↔ | 2*x | ( 2¨* is monadic) | ||
| 2¨*¨.5 | ↔ | 2*.5 | (A constant value) |
This form of composition is particularly useful in providing the monadic cases (both left and right) of dyadic functions, as illustrated above for the square root ( *¨.5) and the powers of two ( 2¨*).
The valence of the derived function is determined by context, and this in turn determines the valence of the argument function as one greater. For example, in the expression *¨.5 (4 9) , the function *¨.5 is monadic, * is dyadic, and the result is the constant 2 3 ; in the expression *¨.5 , the function *¨.5 is niladic (a constant), * is monadic, and the result is the exponential *.5 .
Composition is useful in a wide variety of ways. For example, with one variable argument it provides the monadic cases (both left and right) of dyadic functions, as illustrated above for the powers of two ( 2¨*) and the square root ( *¨.5). An example for the case of two functions is treated in Section 11.
The dual operator is also widely useful.
For example, <\ applied
to a logical vector yields the same vector
with all the 1’s following
the first replaced by zeros,
whereas <\⍢⌽ yields the vector
with all the 1’s
preceding the last replaced by zeros.
Similarly, if f is any function
which applies to columns of a matrix argument,
then
f⍢⍉
applies similarly to rows.
A further important use of the dual is discussed in
Section 10.
Composition with two variables (characters).
This use of composition is modeled on the direct
or ⍺ ⍵ definition form
defined in Elementary Analysis
[2].
It incorporates the same abilities
to define functions with any number of global
(non-explicit) arguments, to prevent side-effects
(by automatically localizing all variables
specified within the defining expression),
and to make conditional and recursive definitions.
The definition is generalized to allow the specification
of the names of explicit arguments in a second argument
(with a jot (∘) for second argument
signifying the use of ⍺ and ⍵),
and to allow the specification of divalent functions.
Thus, f 'b÷x'¨'b'
and
'b÷x'¨'b'
and '⍵÷x'¨∘
'⍵÷x'¨∘
Recursive definition requires the use of the function name in its definition; this name is identified by placing it first in the right argument, separated from the other name or names by a colon. For example, if c←'x×f x-1:x=0:1' , then c¨'f:x' defines the factorial function on non-negative integers. The name f is local and is not associated in any way with the derived function. For the ⍺ ⍵ case c¨∘, the name of the function is denoted by ⍶ , as in c←'⍵×⍶ ⍵-1:⍵=0:1' .
The symbols ⍺ and ⍵ may be used like any other names except that they must not remain as global names in the resulting function. For example, one may use c¨'⍺ ⍵' in lieu of c¨∘ , and 'x+⍺'¨'x ⍺' or '⍵+⍺'¨'⍵ ⍺' for the equivalent of '⍺+⍵'¨∘ .
This form of composition is very convenient for defining and applying functions in computations and for use in theoretical work. For examples:
pol '(⍵∘.*⍳⍴⍺)+.×⍺'¨∘ [8.1]
1 3 3 1 pol 2 4
27 125
1 3 3 1 '(⍵∘.*⍳⍴⍺)+.×⍺'¨∘ 2 4
27 125
spol
'(⍵∘.*⍳⍴⍺)+.×⍺'¨∘ [8.1]
1 3 3 1 pol 2 4
27 125
1 3 3 1 '(⍵∘.*⍳⍴⍺)+.×⍺'¨∘ 2 4
27 125
spol 'c pol ⍵'¨∘
c←1 4 6 4 1
spol 2 4
16 625
'⍺+÷⍵'¨∘/1 2 1 2 (Continued fraction)
1.375
'⍺+÷⍵¨∘\1 2 1 2 (Convergents)
1 1.5 1.333 1.375
f⍨ ↔ '⍵f⍺'¨∘
'(⍺ pol x)×⍵ pol x'¨∘ ↔
'(+⌿(-⍳⍴⍺)⌽⍺∘.×⍵,1↓0×⍺)pol x'¨∘
'c pol ⍵'¨∘
c←1 4 6 4 1
spol 2 4
16 625
'⍺+÷⍵'¨∘/1 2 1 2 (Continued fraction)
1.375
'⍺+÷⍵¨∘\1 2 1 2 (Convergents)
1 1.5 1.333 1.375
f⍨ ↔ '⍵f⍺'¨∘
'(⍺ pol x)×⍵ pol x'¨∘ ↔
'(+⌿(-⍳⍴⍺)⌽⍺∘.×⍵,1↓0×⍺)pol x'¨∘
Divalent functions are defined by catenating the arguments for the monadic and dyadic cases, inserting a pair of colons to separate the two parts. More precisely, if ca¨na and cb¨nb define (not necessarily respectively) monadic and dyadic functions, then (ca,'::',cb)¨na,'::',nb defines the corresponding divalent function. Analogously, (ca,'::',cb)¨∘ defines the divalent function corresponding to ca¨∘ and cb¨∘ . For example:
f g ↔ '(f⍵)+g⍵::(⍺f⍵)+⍺g⍵'¨∘
g ↔ '(f⍵)+g⍵::(⍺f⍵)+⍺g⍵'¨∘
The identity element (or elements)
of a function may be specified
by appending to the name (in the right argument
of ¨)
the symbol ⍳ followed by the appropriate value.
For example,
9. Reduction and Scan
The reduction operator is defined as follows: f/a is an application of the dyadic function f to the set of arguments obtained by indexing a on its last axis. For example, if ⍴a is 4 4 5 , then +.×/a applies the matrix product over the five four-by-four matrices of a to produce a four-by-four result. Similarly, if ⍴a is 4 4 4 5 , then +.×/a yields a result of shape 7⍴4 , and +.×⍤1 2/a yields a result of shape 3⍴4 , and ∘.(+.×⍤1 2)/a yields a result of shape 7⍴4 .
The reduction f⌿a is defined analogously (the indexing applying to the leading axis), as are the scans \ and ⍀ .
The axis operators ⍤ and ⍥ apply to the reduction operator (/ or ⌿) to produce an operator which applies its argument function to the arguments obtained by indexing the specified axis. For example, +.×(/⍤0)a ↔ +.×⌿a .It should be noted that f(\⍤k) and f\[k] are not, in general, equivalent, since the result vectors of the former lie along the last axis of the result rather than along axis k . Similarly, f(/⍤k) and f/[k] are not equivalent in general, although they are for a scalar function f .
10. Scalar Representation
The enclose function (denoted by <) produces a scalar representation of its argument in the sense that the result is of rank zero, and that there exists an inverse function (called disclose, and denoted by >) such that a ↔ ><a for all a . Any result producible by an expression which does not employ the enclose function is called a simple array, or is said to be simple.
Selection and reshaping functions apply without change to non-simple arrays. However, non-simple arrays are outside the domain of all other functions except for enclose, disclose, and equality (together with those functions such as ≠ and ∊ which are defined in terms of equality).
The equality function is extended to non-simple scalar arguments as follows:
| 1. | (<a)≠a for all a | ||
| 2. | If a equals b (in rank, shape, and all elements), then (<a)=(<b) yields 1 |
The enclose function applies to all axes of its argument (i.e., to the entire argument) to produce a single scalar result, but it can also be used in conjunction with the axial operators to apply to units determined by the specified axes. For example, if a←2 3 4 5 ⍴⍳!5 , then m←<⍤1 3 a is a 2 by 4 matrix such that for scalar indices i and j , the element m[i;j] is a non-simple scalar whose disclose (>m[i;j]) is a 3 by 5 simple matrix.
The disclose function is scalar in the sense that it applies to each element of its argument, the new axes disclosed becoming the final axes of the result. For example, using the matrix m of the preceding paragraph, >m is a simple array of shape 2 4 3 5 , and ∧/,(>m)=0 2 1 3 ⍉ a .
The axial operators can also be applied to the disclose function to determine the axes to be disclosed. For example, >⍤1 m produces a result of shape 2 4 5 whose elements are enclosed 3-element vectors.
The disclose function applied to a simple array a produces a result identical to a . Thus (<a)=<>a is a test for whether a is simple.
The expression f⍢> produces a derived function which applies the function f to its argument in an “item-wise” fashion, by disclosing each element of the argument, applying f , and enclosing the result to produce the corresponding element of the overall result. Thus, if r←f⍢>a and q is a particular scalar element of a , then the corresponding element of r is <f>q . In particular, ⍴r equals ⍴a .
11. Derivative Operator
Derivatives apply only to monadic functions, but to functions of any rank r , the derivative f∆ yielding a monadic function of rank (+/r),r . Thus:
| Rank of f | Rank of f∆ | |||
| (Scalar function) | 0 0 | 0 0 (Scalar function) | ||
| (Vector function of a scalar) | 1 0 | 1 1 | ||
| (Scalar function of a vector) | 0 1 | 1 1 (gradient) | ||
| (Vector function v) | 1 1 | 2 1 (Matrix of partials) | ||
| (v∆) | 2 1 | 3 1 (v∆ ∆) |
The shape of f∆ is determined as follows: if u is a unit of f , then ⍴ f∆ u is (⍴ f u),⍴u .
The derivative operator together with composition and scalar operators can be used to express the familiar differentiation rules as follows:
f g∆ ↔ f∆
g∆ ↔ f∆ (g∆)
f
(g∆)
f g∆ ↔ f∆
g∆ ↔ f∆ g
g (g∆
(g∆ f)
f¨g∆ ↔ f∆¨g
f)
f¨g∆ ↔ f∆¨g (g∆)
÷¨g∆ ↔ -¨(g∆)
(g∆)
÷¨g∆ ↔ -¨(g∆)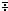 (g
(g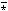 2)
*¨n∆ ↔ *¨(n-1)
2)
*¨n∆ ↔ *¨(n-1) n
*∆ ↔ *
n
*∆ ↔ *
12. Difference Operator
The derivative operator ∆ discussed in the preceding section actually yields a divalent result, the dyadic form being the difference function defined as follows:
s f∆ x ↔ ((f x+s)-f x)÷s
This function is also completed at zero so that the expression 0 f∆ x equals the derivative f∆ x .
13. Dyadic Reduction and Scan
If f is a function, then f/ and f\ produce divalent derived functions whose dyadic forms are defined here. If r←k f/x and (k≥0)∧k≤⍴x , then ⍴r is 1+(⍴x)-k , and r[i] is f/k↑i↓x . Moreover, (-k)f/x is the dual of k f/x with respect to reversal, in the following sense:
(-k)f/x ↔ ⌽k f/ ⌽x
Thus 2 -/x and ¯2 -/x yield backward and forward differences of x , respectively. More generally, 2 f/x and ¯2 f/x yield “pairwise” applications of f . For example, ¯2 ÷/t yields the ratios of terms in a series, and ^/2=/v determines whether all elements of v are equal.
The new coordinate of the result produced by the dyadic form precedes those of the monadic form. Thus if s is the shape of f/x , then the shape of k f/ x has the form n,s . Moreover, (⍴x) f/x is equivalent to f/x except that the shape of the result has a leading element of 1 .
The dyadic form of f\ is defined similarly, differing only in that it includes the reductions over all leading prefixes so as to yield a result of the same length as the argument x . More precisely, if r←k f\x , then ⍴r is ⍴x and:
r[i] ↔ f/((|k)⌊i+1)↑(0⌈i-(|k)-1)↓x
For example, ¯2 -\x yields the forward differences of x but includes the leading element of x so that +\ is a true inverse, that is,
+\¯2-\x ↔ x
¯2-\+\x ↔ x
14. The Variant Operator
Certain functions have variants, in the sense that there exist other closely related functions. For example, the sine of an argument in radians and the sine of an argument in degrees are variants. Moreover, in current APL each of the functions dependent on index origin has two variants (chosen by ⎕io) and each relation has many variants (specified by ⎕ct).
We now introduce a dyadic variant operator
denoted by 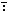 and called mark
whose right argument specifies the particular variant.
Functions are treated in seven classes as follows:
and called mark
whose right argument specifies the particular variant.
Functions are treated in seven classes as follows:
| 1) |
Dyadic circular functions with left arguments 1 , 2 , 3 , ¯1 , ¯2 , ¯3 . ○ Thus the right argument d
gives the number of divisions
in a right angle and,
in particular, ○ | |||||||||||||||||
| 2) |
Relations f | |||||||||||||||||
| 3) |
Indexing (monadic and dyadic ⍳ and subscripting) ⍳ | |||||||||||||||||
| 4) |
Random (monadic and dyadic ?) The right argument is a function which specifies the distribution or a character which selects one of several standard distribution as follows:
This variant also takes an integer right argument
to determine the origin of the population,
as in | |||||||||||||||||
| 5) |
Residue arithmetic (dyadic +,-,×,* , and monadic -) x f In particular, since 0|x ↔ x ,
we have f | |||||||||||||||||
| 6) |
The functions take and expand
insert at certain positions
a “fill element”
(blank for characters, and zero for numeric);
the variant operator allows
the specification of this element,
as in ↑ | |||||||||||||||||
| 7) |
The conformability requirements
for catenation can be relaxed
by “padding” either argument
along the axes complementary
to the catenation axis,
using overtakes and some specified fill element.
This is provided by the variant operator,
the right argument being the fill element,
or a jot indicating the default fill elements blank or zero.
For example, m, |
For any function f dominated
by the variant operator,
the function f alone
is treated as a default case,
the default value being given
by a system variable.
For the relations, this system variable
is ⎕ct ,
and therefore ≤ ↔ ≤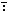 ⎕ct .
⎕ct .
The default for the functions ⍳ , ? , and [ is determined by ⎕io , and for the remaining cases we introduce new system variables as follows:
| Circular Functions: | ⎕cf | ○.5 | |||
| Residue Arithmetic: | ⎕ra | 0 | |||
| Type of Distribution: | ⎕dt | 'r' | |||
| Fill Element: | ⎕fe | 0 |
The rightmost column shows the values in a clear workspace.
15. Boolean Operator
The boolean operator  is an example of a useful monadic function
having a numeric argument.
Applied to an integer i∊⍳16
it produces the “ith boolean function”
according to the following definition:
is an example of a useful monadic function
having a numeric argument.
Applied to an integer i∊⍳16
it produces the “ith boolean function”
according to the following definition:
i ↔ 2⊥,0 1∘.(i )0 1
)0 1
Thus 1 ↔ ∧
and 7
↔ ∧
and 7 ↔ ∨ ,
and in general, ~¨(i
↔ ∨ ,
and in general, ~¨(i ) ↔ (15-i)
) ↔ (15-i) .
The use of a vector i produces a vector function.
.
The use of a vector i produces a vector function.
16. Set Functions
We define seven set functions as follows:
| Nub | ∪w | ((⍳⍴w)=w⍳w)/w←,w | ||
| Ordered Nub | ∩w | w[⍋w←∪w] | ||
| Distribution | 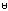 w w |
(∪w)∘.=w | ||
| Ordered Distribution | 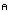 w w |
(∩w)∘.=w | ||
| Union | v∪w | (,v),,w | ||
| Intersection | v∩w | ((,v)∊,w)/,v | ||
| Difference | v~w | (~(,v)∊,w)/,v | ||
| Inclusion | v⊆w | ^/(,v)∊,w | ||
| v⊇w | w⊆v | |||
| Strict Inclusion | v⊂w | (v⊆w)^~v⊇w | ||
| v⊃w | w⊂v |
Practical and theoretical application of
the distribution functions will now be illustrated.
If v is a
vector with repeated elements
and f is a scalar function,
then every distinct element of f v
is contained in f∪v ,
and these elements can be “distributed”
to the positions their arguments occupied in v
by the expression (f∪v)+.×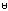 v
Thus:
v
Thus:
f v ↔ (f∪v)+.×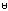 v [16.1]
v [16.1]
If the evaluation of f is time-consuming, and if ⍴∪v is considerably less than ⍴v , this identity can provide an efficient algorithm for the evaluation of f v . Similar remarks apply to the ordered nub and the ordered distribution matrix.
The product of the sum of two vectors a and b (that is, ×/a+b) can be “expanded” to an equivalent sum of 2*⍴b terms, in which a typical term is a product of ⍴b factors, one chosen from each position of either a or b. Formally, each term is of the form (a×.*~l)×(b×.*l) where l is a logical vector of shape ⍴b . All terms are therefore obtained by replacing l by the matrix t←(k⍴2)⊤⍳2*k←⍴b of all such logical vectors. We therefore have the identity:
×/a+b ↔ (a×.*~t)+.×(b×.*t←(k⍴2)⊤⍳2*k←⍴b)
For a scalar x , the expression ×/x-r yields the value of a polynomial with roots r evaluated at x . By substituting x for a and -r for b in the foregoing identity, and using the fact that (for a scalar x) the expressions x×.*l and x*+/l are identical, we can derive a sequence of equivalent expressions which finally yield a relation between the coefficients and the roots of a polynomial:
×/x-r (x×.*~t)+.×(b×.*t←(k⍴2)⊤⍳2*k←⍴b←-r) (x*s←+⌿~t)+.×(b×.*t) ((x*∩s)+.×s)+.×(b×.*t) 16.1 (x*∩s)+.×((
s)+.×(b×.*t)) +.× is assoc (x*⍳1+⍴b)+.×((
s)+.×(b×.*t)) ∩s ↔ ⍳1+⍴b ((
s)+.×(b×.*t)) pol x pol in 8.1
The left argument of pol above is therefore the coefficient vector of the polynomial whose roots are r . Consequently, a function cfr , which yields the coefficients when applied to the vector of roots, may be defined as follows:
cfr '(
'(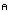 +⌿~t)+.×(-⍵)×.*t←(k⍴2)⊤⍳2*k←⍴⍵'¨∘
+⌿~t)+.×(-⍵)×.*t←(k⍴2)⊤⍳2*k←⍴⍵'¨∘
The definition of cfr is, of course, a definition of Newton’s symmetric functions.
As a final example of the use of the (ordered) distribution function, we state the shape of the transpose i⍉a as follows:
⍴i⍉a ↔ (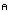 i)⌊.(⌊⍣∘)⍨⍴a
i)⌊.(⌊⍣∘)⍨⍴a
17. Indexing
The range of indexing will now be extended to include negative numbers in a manner which makes it possible to refer to an index position by two different numbers, one relative to its position as counted forward, and one (non-positive) relative to its position as counted backward: an axis of length n may be indexed by any of the elements of (⍳2×n)-n , the position indexed by i being i+n×i<0 . Thus:
n←4
⎕io←1
⎕←i←(⍳2×n)-n
¯3 ¯2 ¯1 0 1 2 3 4
i+n×i<0
1 2 3 4 1 2 3 4
⎕io←0
⎕←i←(⍳2×n)-n
¯4 ¯3 ¯2 ¯1 0 1 2 3
i+n×i<0
0 1 2 3 0 1 2 3
For example, in 0-origin, x[¯1] ↔ x[¯1+⍴x] , and selects the last element of x . Similarly, in 1-origin, x[0] selects the last element.
We also introduce a form of indexing called from denoted by ⌷ , and of rank 0,1,rr , where r is the rank of the right argument. The basic definition is:
i⌷a ↔ (,a)[⍉(⍴a)⊥⍉i]
The function ⌷ distributes
over any scalar function;
thus, i⌷a+b ↔ (i⌷a)+(i⌷b) .
The right argument of the axis operator applied to ⌷ is of the form i,_,j . For example:
m←3 4⍴⍳12
m
0 1 2 3
4 5 6 7
8 9 10 11
2 2 ⌷ m
10
2 ⌷⍤_ 1 m
2 6 10
2 0 1 ⌷⍤_ 1 m
2 4 9
(3 2⍴3|⍳6)⌷m
1 8 6
The use of the indexing function will be illustrated in a proof of the useful identity i⍉j⍉a ↔ i[j]⍉a . We first state the definition of the transpose as follows: if k is any vector index of j⍉a then
k⌷j⍉a ↔ k[j]⌷a
Then:
k⌷i⍉j⍉a
k[i]⌷j⍉a
(k[i])[j]⌷a
k[i[j]]⌷a
k⌷i[j]⍉a
References
| 1. | APL Language, Form Number GC26-3847, IBM Corporation. | |
| 2. | Iverson, K. E., Elementary Analysis, APL Press, 1976. |
Index of Symbols
| Symbol | Class | Description | Section | |||
 | function assignment | 0 | ||||
| ∘ | “monadic case” symbol | 1 | ||||
| _ | variable | infinity | 1 | |||
| ¯ | variable | negative infinity | 1 | |||
| ⍣ | operator | power | 2 | |||
| ⍨ | operator | commute | 3 | |||
 | operator | scalar | 4 | |||
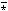 | operator | scalar | 4 | |||
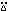 | operator | domain | 5 | |||
| ⍤ | operator | nuax | 7 | |||
| ⍥ | operator | coax | 7 | |||
| ⍢ | operator | dual | 8 | |||
| ¨ | operator | composition | 8 | |||
| ⍺ | left argument | 8 | ||||
| ⍵ | right argument | 8 | ||||
| : | separator | 8 | ||||
| ⍶ | recursive definition | 8 | ||||
| :: | monadic/dyadic separator | 8 | ||||
| ⍳ | identity element | 8 | ||||
| / | operator | reduction | 9, 13 | |||
| \ | operator | scan | 9, 13 | |||
| ⌿ | operator | reduction | 9 | |||
| ⍀ | operator | scan | 9 | |||
| < | function | enclose | 10 | |||
| > | function | disclose | 10 | |||
| ∆ | operator | derivative/difference | 11, 12 | |||
 | operator | scalar | 11 | |||
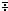 | operator | scalar | 11 | |||
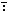 | operator | variant | 14 | |||
| ⎕cf | variable | circular functions | 14 | |||
| ⎕ra | variable | residue arithmetic | 14 | |||
| ⎕dt | variable | type of distribution | 14 | |||
| ⎕fe | variable | fill element | 14 | |||
 | operator | boolean | 15 | |||
| ∪ | function | nub/union | 16 | |||
| ∩ | function | ordered nub/intersection | 16 | |||
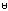 | function | distribution | 16 | |||
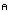 | function | ordered distribution | 16 | |||
| ~ | function | difference | 16 | |||
| ⊆ | function | inclusion | 16 | |||
| ⊇ | function | inclusion | 16 | |||
| ⊂ | function | strict inclusion | 16 | |||
| ⊃ | function | strict inclusion | 16 | |||
| ⌷ | function | indexing | 17 |
Errata
| • | In Section 2, in the first paragraph, it should say f⍣k ↔ f f⍣(k-1) instead of f⍣k ↔ f f⍣k-1 . | ||||||||||
| • |
In Section 4, the opening paragraph should end with
“... by the definition
for  ”
instead of “... by the definition for +”. ”
instead of “... by the definition for +”.
| ||||||||||
| • | In Section 5, in the closing paragraph, it should say “divalent function f” instead of “bivalent function f”. | ||||||||||
| • |
In Section 6, the closing paragraph has several
errors that can be corrected in a variety of ways,
such as:
| ||||||||||
| • | In Section 7, in the last sentence of the third paragraph, it should say k⌽⍤ _ 3 a instead of k⌽⍤ _3 a . | ||||||||||
| • | In Section 8, in the opening sentence, it should say De Morgan instead of deMorgan. | ||||||||||
| • | In Section 8, in the opening sentence, it should say “the extension being to include a monadic right argument” instead of “the extension being to include a monadic left argument”. | ||||||||||
| • | In Section 8, in the “Duality and simple composition” subsection, in the paragraph that begins with “In the dyadic case of the composition above” (the third paragraph), it should say “valences” instead of “valencies”. | ||||||||||
| • | In Section 8, in the examples of composition, the result of spol 2 4 should be 81 625 instead of 16 625 . | ||||||||||
| • |
In Section 8, in the penultimate paragraph,
it should say (ca,'::',cb)¨(na,'::',nb) instead of (ca,'::',cb)¨na,'::',nb | ||||||||||
| • | In Section 10, the description of how axial operators apply to the disclose function contradicts the characterization that the disclose function is scalar. | ||||||||||
| • |
In Section 14, item 3) should include
the new indexing function
such that ⌷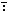 k
specifies origin k . k
specifies origin k .
| ||||||||||
| • |
In Section 14, the text says that
dyadic ⍳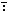 k
specifies the origin but is silent on
whether comparison tolerance can be effected.
Presumably, similar
to ? k
specifies the origin but is silent on
whether comparison tolerance can be effected.
Presumably, similar
to ?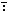 'g' 'g'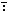 1
in item 4) specifying a Gaussian distribution with
origin 1 , ⍳ 1
in item 4) specifying a Gaussian distribution with
origin 1 , ⍳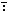 k k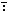 t
or ⍳ t
or ⍳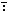 t t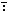 k
can specify indexing with origin k and
comparison tolerance t .
Alternatively, k
can specify indexing with origin k and
comparison tolerance t .
Alternatively, 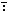 (k,t) (k,t) | ||||||||||
| • | In Section 14, the default fill element (the value of ⎕fe in a clear workspace) should be ∘ rather than 0 , so that take and expand on character arguments would give expected results. | ||||||||||
| • |
In Section 15, the opening sentence should say that
“the boolean operator  is an example of a monadic operator” rather than
“the boolean operator
is an example of a monadic operator” rather than
“the boolean operator  is an example of a monadic function”.
is an example of a monadic function”.
| ||||||||||
| • | In Section 16, the opening sentence should say “We define eleven set functions ...” instead of “We define seven set functions ...”. | ||||||||||
| • |
In Section 16, the last line should say ⍴i⍉a ↔ ( 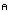 i)⌊.(⌊⍣∘) ⍴a i)⌊.(⌊⍣∘) ⍴a instead of ⍴i⍉a ↔ ( 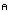 i)⌊.(⌊⍣∘)⍨⍴a i)⌊.(⌊⍣∘)⍨⍴a | ||||||||||
| • | In Section 17, in the opening paragraph and in the first displayed example, for the position indexed by i , it should say i+n×i<⎕io instead of i+n×i<0 . | ||||||||||
| • | In Section 17, the equivalence x[¯1] ↔ x[¯1+⍴x] ignores the fact that x[¯1] is a scalar whereas x[¯1+⍴x] is a vector. | ||||||||||
| • | In Section 17, it should say that the function ⌷ has ranks 0,1,r rather than 0,1,rr . (Actually, it should say that ⌷ has ranks 0 1 _ , but the notion of infinite rank is undeveloped in the paper. See Section 6.) | ||||||||||
Originally appeared as IBM Research Report RC 7091 (#30399), 1978-04-26.
| created: | 2009-03-09 16:25 |
| updated: | 2021-05-30 21:55 |