Chapter 9: Trains of Verbs
In this chapter we continue the topic of trains of verbs begun in Chapter 03. Recall that a train is an isolated sequence of functions, written one after the other, such as (+ * -).9.1 Review: Monadic Hooks and Forks
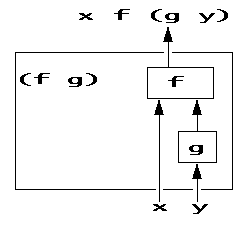
Recall from Chapter 03 the monadic hook, with the scheme:
(f g) y means y f (g y)
Here is an example, as a brief reminder: a whole number
is equal to its floor:
| y =: 2.1 3 | <. y | y = <. y | (= <.) y |
| 2.1 3 | 2 3 | 0 1 | 0 1 |
Recall also the monadic fork, with the scheme:
(f g h) y means (f y) g (h y)
For example: the mean of a list of numbers is the sum divided by the number-of-items:
sum =: +/ mean =: sum % #
| y =: 1 2 3 4 | sum y | # y | (sum y) % (# y) | mean y |
| 1 2 3 4 | 10 | 4 | 2.5 | 2.5 |
Now we look at some further variations.
9.2 Dyadic Hooks
3 hours and 15 minutes is 3.25 hours. A verb hr, such that (3 hr 15) is 3.25, can be written as a hook. We want x hr y to be x + (y%60) and so the hook is:hr =: + (%&60) 3 hr 15 3.25The scheme for dyadic hook is:
x (f g) y means x f (g y)
with the diagram:
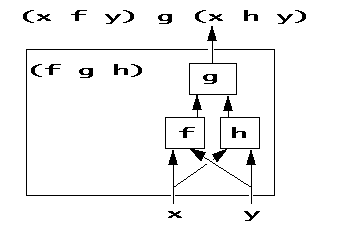
9.3 Dyadic Forks
Suppose we say that the expression "10 plus or minus 2" is to mean the list 12 8. A verb to compute x plus-or-minus y can be written as the fork (+,-):
| (10+2) , (10-2) | 10 (+,-) 2 |
| 12 8 | 12 8 |
The scheme for a dyadic fork is:
x (f g h) y means (x f y) g (x h y)
Here is a diagram for this scheme:
9.4 Review
There are four basic schemes for trains of verbs.
(f g h) y = (f y) g (h y) monadic fork
x (f g h) y = (x f y) g (x h y) dyadic fork
(f g) y = y f (g y) monadic hook
x (f g) y = x f (g y) dyadic hook
9.5 Longer Trains
Now we begin to look at ways to broaden the class of functions which can be defined as trains. In general a train of any length can be analysed into hooks and forks. For a train of 4 verbs, e f g h, the scheme is that
e f g h means e (f g h)
that is, a 4-train (e f g h) is a hook, where the first verb is e and the
second is the fork (f g h).
For example, Suppose that y is a list of numbers:
y =: 2 3 4Then the "norm" of y is defined as (y - mean y), where mean is defined above as (sum % #). We see that the following expressions for the norm of y are all equivalent:
y - mean y _1 0 1 (- mean) y NB. as a hook _1 0 1 (- (sum % #)) y NB. by definition of mean _1 0 1 (- sum % #) y NB. as 4-train _1 0 1A certain amount of artistic judgement is called for with long trains. This last formulation as the 4-train (- sum % #) does not bring out as clearly as it might that the key idea is subtracting the mean. The formulation ( - mean) is clearer.
For a train of 5 verbs d e f g h the scheme is:
d e f g h means d e (f g h)
That is, a 5-train (d e f g h) is a fork with first verb d, second verb e and
third verb the fork (f g h)
For example, if we write a calendar date in the form day month year:
date =: 28 2 1999and define verbs to extract the day month and year separately:
Da =: 0 & {
Mo =: 1 & {
Yr =: 2 & {
the date can be presented in different ways by 5-trains:
| (Da , Mo , Yr) date | (Mo ; Da ; Yr) date |
| 28 2 1999 | +-+--+----+ |2|28|1999| +-+--+----+ |
The general scheme for a train of verbs (a b c ...) depends upon whether the number of verbs is even or odd:
even: (a b c ...) means hook (a (b c ...))
odd : (a b c ...) means fork (a b (c ...))
9.6 Identity Functions
There is a built-in verb, monadic [ (left bracket, called "Same"). It gives a result identical to its argument.
| [ 99 | [ 'a b c' |
| 99 | a b c |
There is a dyadic case, and also a similar verb ] . Altogether we have these schemes:
[ y means y
x [ y means x
] y means y
x ] y means y
| [ 3 | 2 [ 3 | ] 3 | 2 ] 3 |
| 3 | 2 | 3 | 3 |
Monadic [ and monadic ] are both called "Same". Dyadic [ is called "Left". Dyadic ] is "Right".
The expression (+ % ]) is a fork; for arguments x and y it computes:
(x+y) % (x ] y)
that is,
(x+y) % y
| 2 ] 3 | (2 + 3) % (2 ] 3) | 2 (+ % ]) 3 |
| 3 | 1.66667 | 1.66667 |
Another use for the identity function [ is to cause the result of an assignment to be displayed. The expression foo =: 42 is an assignment while the expression [ foo =: 42 is not: it merely contains an assignment.
foo =: 42 NB. nothing displayed
[ foo =: 42
42
Yet another use for the [ verb is to allow several assignments to be combined
on one line.
| a =: 3 [ b =: 4 [ c =: 5 | a,b,c |
| 3 | 3 4 5 |
Since [ is a verb, its arguments must be nouns, (that is, not functions). Hence the assignments combined with [ must all evaluate to nouns.
9.6.1 Example: Hook as Abbreviation
The monadic hook (g h) is an abbreviation for the monadic fork ([ g h). To demonstrate, suppose we have:g =: , h =: *: y =: 3Then each of the following expressions is equivalent.
([ g h) y NB. a fork 3 9 ([ y) g (h y) NB. by defn of fork 3 9 y g (h y) NB. by defn of [ 3 9 (g h) y NB. by defn of hook 3 9
9.6.2 Example: Left Hook
Recall that the monadic hook has the general scheme
(f g) y = y f (g y)
How can we write, as a train, a function with the scheme
( ? ) y = (f y) g y
There are two possibilities. One is the fork (f g ]):
f =: *:
g =: ,
(f g ]) y NB. a fork
9 3
(f y) g (] y) NB. by meaning of fork
9 3
(f y) g y NB. by meaning of ]
9 3
For another possibility, recall the ~ adverb with its scheme:
(x f~ y) means y f x
Our train can be written as the hook (g~ f).
(g~ f) y NB. a hook 9 3 y (g~) (f y) NB. by meaning of hook 9 3 (f y) g y NB. by meaning of ~ 9 3
9.6.3 Example: Dyad
There is a sense in which [ and ] can be regarded as standing for left and right arguments.f =: 'f' & , g =: 'g' & ,
| foo =: (f @: [) , (g @: ]) | 'a' foo 'b' |
| f@:[ , g@:] | fagb |
9.7 The Capped Fork
The class of functions which can be written as unbroken trains can be widened with the aid of the "Cap" verb [: (leftbracket colon)The scheme is: for verbs f and g, the fork:
[: f g means f @: g
For example, with f and g as above, we have
| y=:'y' | f g y | (f @: g) y | ([: f g) y |
| y | fgy | fgy | fgy |
Notice how the sequence of three verbs ([: f g) looks like a fork, but with this "capped fork" it is the MONADIC case of the middle verb f which is applied.
The [: verb is valid ONLY as the left-hand verb of a fork. It has no other purpose: as a verb it has an empty domain, that is, it cannot be applied to any argument. Its usefulness lies in building long trains. Suppose for example that:
h =: 'h'&,then the expression (f , [: g h) is a 5-train which denotes a verb:
(f , [: g h) y NB. a 5-train fyghy (f y) , (([: g h) y) NB. by meaning of 5-train fyghy (f y) , (g @: h y) NB. by meaning of [: fyghy (f y) , (g h y) NB. by meaning of @: fyghy 'fy' , 'ghy' NB. by meaning of f g h fyghy
9.8 Constant Functions
Here we continue looking at ways of broadening the class of functions that we can write as trains of verbs. There is a built-in verb 0: (zero colon) which delivers a value of zero regardless of its argument. There is a monadic and a dyadic case:
| 0: 99 | 0: 2 3 4 | 0: 'hello' | 88 0: 99 |
| 0 | 0 | 0 | 0 |
As well as 0: there are similar functions 1: 2: 3: and so on up to 9: and also the negative values: _9: to _1:
| 1: 2 3 4 | _3: 'hello' |
| 1 | _3 |
0: is said to be a constant function, because its result is constant. Constant functions are useful because they can occur in trains at places where we want a constant but must write a verb, (because trains of verbs, naturally, contain only verbs).
For example, a verb to test whether its argument is negative (less than zero) can be written as (< & 0) but alternatively it can be written as a hook:
negative =: < 0:
| x =: _1 0 2 | 0: x | x < (0: x) | negative x |
| _1 0 2 | 0 | 1 0 0 | 1 0 0 |
9.9 Constant Functions with the Rank Conjunction
The constant functions _9: to 9: offer more choices for ways of defining trains. Neverthless they are limited to single-digit scalar constants. We look now at at a more general way of writing constant functions. Suppose that k is the constant in question:k =: 'hello'An explicit verb written as (3 : 'k') will give a constant result of k:
| k | (3 : 'k') 1 | (3 : 'k') 1 2 |
| hello | hello | hello |
Since the verb (3 : 'k') is explicit, its rank is infinite. To apply it separately to scalars then (as we saw in Chapter 07) we need to specify a rank R of 0, with the aid of the Rank conjunction " :
| k | R =: 0 | ((3 : 'k') " R) 1 2 |
| hello | 0 | hello hello |
The expression ((3 : 'k') " R) can be abbreviated as (k " R), because " can take, as its left argument, a verb, as above, or a noun:
| k | R | ((3 : 'k') " R) 1 2 | ('hello' " R) 1 2 |
| hello | 0 | hello hello |
hello hello |
Note that if k is a noun, then the verb (k"R) means: the constant value k produced for each rank-R cell of the argument. By contrast, if v is a verb, then the verb (v"R) means: the verb v applied to each rank-R cell of the argument.
The general scheme for constant functions with " is:
k " R means (3 : 'k') " R
9.9.1 A Special Case
Given a temperature in degrees Fahrenheit, the equivalent in Celsius is computed by subtracting 32 and multiplying by five-ninths.Celsius =: ((5%9) & *) @: (- &32) Celsius 32 212 0 100Another way to define Celsius is as a fork - a train of three verbs.
Celsius =: (5%9 "_ ) * (-&32) Celsius 32 212 0 100Notice that the fork in Celsius above has its left verb as a constant function. Here we have a special case of a fork which can be abbreviated in the form (noun verb verb).
Celsius =: (5%9) * (-&32) Celsius 32 212 0 100The general scheme (new in J6) for this abbreviation for a fork is: if n is a noun, u and v are verbs, then
n u v means the fork (n"_) u v
We have come to the end of of Chapter 9.