15. Central Limit Theorem

An illustration of the central limit theorem, that the sum of independent random variables converges to the normal distribution [51b].

   t←¯1+{≢⍵}⌸(⍳41),(5×⍳40)⍸+⌿?10 1e6⍴21
   ⍴t
41
   5 8⍴t
    0     0     0     0      0     13    28    90
  317   894  2095  4574   8671  15001 24338 36728
51254 66804 82787 93943 101045 101752 96510 85281
70418 54506 39802 27267  16964   9764  5031  2467
 1059   422   136    32      6      1     0     0

t counts the number of occurrences in the intervals with endpoints 5×⍳40 , of 1e6 samples from the sum of ten repetitions of ?21 . A plot of t :

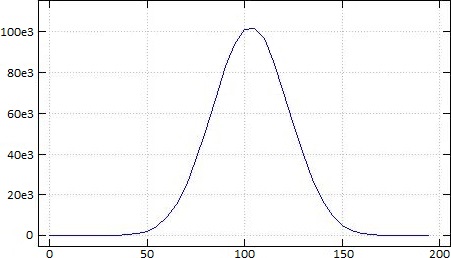
The derived function {≢⍵}⌸x counts the number of occurrences of each unique cell of x . On 1-byte integers the computation takes only 1.4 times as long as required for the apparently simpler problem ⌈/x . Thinking about an obvious C implementation for {≢⍵}⌸x leads to a non-obvious implementation for ⌈/x [15a] faster than

max=*x++; for(i=1;i<n;++i){if(max<*x)max=*x; ++x;}