A History of APL in 50 Functions

16. A Memo Operator

Jay sent out an e-mail asking who would be interested to go see the film The Man Who Knew Infinity [56]. Fiona’s response: Ah, Mr. 1729; I’m in. John was game, and so was I.

Partition Function

Nik found an essay by Stephen Wolfram [55] on Ramanujan written on occasion of the film, wherein Wolfram said:

A notable paper [Ramanujan] wrote with Hardy [56] concerns the partition function (PartitionsP in the Wolfram Language) that counts the number of ways an integer can be written as a sum of positive integers. The paper is a classic example of mixing the approximate with the exact. The paper begins with the result for large n: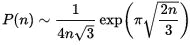

But then, using ideas Ramanujan developed back in India, it progressively improves the estimate, to the point where the exact integer result can be obtained. In Ramanujan’s day, computing the exact value of PartitionsP[200] was a big deal — and the climax of his paper. But now, thanks to Ramanujan’s method, it’s instantaneous:
In[1]:= PartitionsP[200]
Out[1]= 3 972 999 029 388

A partition [57] of a non-negative integer n is a vector v of positive integers such that n = +/v, where the order in v is not significant. For example, the partitions of the first six non-negative integers are:

┌┐
││
└┘
┌─┐
│1│
└─┘
┌─┬───┐
│2│1 1│
└─┴───┘
┌─┬───┬─────┐
│3│2 1│1 1 1│
└─┴───┴─────┘
┌─┬───┬───┬─────┬───────┐
│4│3 1│2 2│2 1 1│1 1 1 1│
└─┴───┴───┴─────┴───────┘
┌─┬───┬───┬─────┬─────┬───────┬─────────┐
│5│4 1│3 2│3 1 1│2 2 1│2 1 1 1│1 1 1 1 1│
└─┴───┴───┴─────┴─────┴───────┴─────────┘

Can we compute the partition counting function “instantaneously” in APL?

We will use a recurrence relation derived from the pentagonal number theorem, proved by Euler more than 160 years before Hardy and Ramanujan:

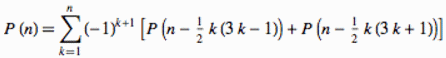
equation (11) in [58]. In APL:

   pn  ← {1≥⍵:0≤⍵ ⋄ -/+⌿∇¨rec ⍵}
   rec ← {⍵ - (÷∘2 (×⍤1) ¯1 1 ∘.+ 3∘×) 1+⍳⌈0.5*⍨⍵×2÷3}

   pn¨ 0 1 2 3 4 5
1 1 2 3 5 7

   pn 30
5604

Warning: don’t try pn 200 because that would take a long time. Why? pn 200 engenders pn being applied to each element of rec 200 and:

   rec 200
199 195 188 178 165 149 130 108 83 55 24 ¯10
198 193 185 174 160 143 123 100 74 45 13 ¯22

Each of the non-negative values would itself engender further recursive applications.

A Memo Operator

I recalled from J the memo adverb (monadic operator) M. . Paraphrasing the J dictionary [59, 51c]: f M is the same as f but may keep a record of the arguments and results for reuse. It is commonly used for multiply-recursive functions. Sounds like just the ticket!

The Functionistas had previously implemented a (dyadic) memo operator [60]. The version here is more restrictive but simpler. The restrictions are as follows:

The cache is constructed “on the fly” and is discarded once the operand finishes execution.
The operand is a dfn {condition:basis ⋄ expression} where none of condition , base , and expression contain a ⋄ and recursion is denoted by ∇ in expression .
The arguments are scalar integers.
The operand function does not have ¯1 as a result.
A recursive call is on a smaller integer.

With these restrictions, our memo operator can be defined as follows:

M←{
 f←⍺⍺
 i←2+'⋄'⍳⍨t←3↓,⎕cr 'f'
 0=⎕nc '⍺':⍎' {T←(1+  ⍵)⍴¯1 ⋄  {',(i↑t),'¯1≢T[⍵]  :⊃T[⍵]   ⋄ 
                                        ⊃T[⍵]  ←⊂',(i↓t),'⍵}⍵'
           ⍎'⍺{T←(1+⍺,⍵)⍴¯1 ⋄ ⍺{',(i↑t),'¯1≢T[⍺;⍵]:⊃T[⍺;⍵] ⋄ 
                                        ⊃T[⍺;⍵]←⊂',(i↓t),'⍵}⍵'
}

   pn M 10
42
   pn 10
42

Obviously, the ⍎ lines in M are crucial. When the operand is pn , the executed expression is as follows; the characters inserted by M are shown in red.

{T←(1+⍵)⍴¯1 ⋄ {1≥⍵:0≤⍵ ⋄ ¯1≢T[⍵]:⊃T[⍵] ⋄ ⊃T[⍵]←⊂-/+⌿∇¨rec ⍵}⍵}⍵

The machinations produce a worthwhile performance improvement:

   pn M 30
5604
   cmpx 'pn M 30'
3.94e¯4
   cmpx 'pn 30'
4.49e1 
   4.49e1 ÷ 3.94e¯4
113959

That is, pn M 30 is faster than pn 30 by a factor of 114 thousand.

Can APL compute pn M 200 “instantaneously”? Yes it can, for a suitable definition of “instantaneous”.

   cmpx 'm←pn M 200'
4.47e¯3
   m
3.973e12
   0⍕m
 3972999029388

How long would pn 200 have taken without a memo operator? A lower bound derives by counting the number of function calls:

   pn ← {1≥⍵:0≤⍵ ⋄ -/+⌿∇¨rec ⍵}
   pnc← {1≥⍵:1 ⋄ 1++/∇¨,rec ⍵}    ⍝ # of function calls

   pnc¨ ⍳15
1 1 5 9 17 29 49 87 149 261 451 781 1351 2333 4041
   pnc M¨ ⍳15
1 1 5 9 17 29 49 87 149 261 451 781 1351 2333 4041

pnc counts the number of function calls required by pn , and is in the form {condition:basis ⋄ expression} that M can handle. Extrapolating that pn 30 took 45 seconds to compute:

   pnc M¨ 30 200
2.59912e7 7.5715e47
   ⊢ s ← 45 × ÷⍨/ pnc M¨ 30 200    ⍝ # of seconds
1.3109e42
   s ÷ ×/ 365.2425 24 60 60        ⍝ # of years
4.15407e34

The algorithm pn M can compute the number of partitions for large n rapidly and exactly if extended precision arithmetic were available. From J:

   timer 'pn M. 1000'
0.0524486

   pn M. 1000
24061467864032622473692149727991

M also works on operands which are anonymous, dyadic, or have non-scalar results.

Anecdote

On 2016-10-15 I presented A Tour (de Force) of APL in 16 Expressions at Functional Conf 2016 at Bengalore, India [6]. I introduced the above section by saying, “After coming all this way to within 200 miles of Kumbakonam, of course I have to talk about Ramanujan.”

On leaving Bangalore, the passport control officer I dealt with had “S. Srinivasa” on his name tag. I asked him if he knew of Ramanujan. He smiled and said yes. It turned out he was a distant relative of Ramanujan.

Presented in [61, 5, 6].