36. Fibonacci Numbers

The n-th element of the sequence 0 1 1 2 3 5 8 13 21 34 55 … can be computed in a variety of ways:

Double Recursion

   fib←{1≥⍵:⍵ ⋄ (∇⍵-2)+∇⍵-1}

   fib¨ ⍳10
0 1 1 2 3 5 8 13 21 34

Like other multiple recursions, this function can be made more efficient by use of the memo operator:

   fib M¨ ⍳10
0 1 1 2 3 5 8 13 21 34

   cmpx 'fib 30' 'fib M 30'
  fib 30   → 1.44E0  |    0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
  fib M 30 → 1.50E¯3 | -100% 

Single Recursion

   fib1←{⍺←0 1 ⋄ 0=⍵:⊃⍺ ⋄ (1↓⍺,+/⍺)∇⍵-1}

   fib1¨ ⍳10
0 1 1 2 3 5 8 13 21 34

Iteration

   fib2←{⊃+\∘⌽⍣⍵⍳2}

   fib2¨ ⍳10
0 1 1 2 3 5 8 13 21 34

Power of Phi

Power of the golden ratio φ (2÷⍨1+5*0.5). Because of the limited precision of 64-bit IEEE floating-point numbers this method is good only for n up to 70.

   fib3←{⌊0.5+r÷⍨(2÷⍨1+r←5*0.5)*⍵}

   fib3¨ ⍳10
0 1 1 2 3 5 8 13 21 34

Continued Fractions

   fib4←{1∧+∘÷/0,⍵⍴1}

   fib4¨ ⍳10
0 1 1 2 3 5 8 13 21 34

Sum of Binomial Coefficients

   fib5← ⍳ +.! ⌽∘⍳

   fib5¨ ⍳10
0 1 1 2 3 5 8 13 21 34

Matrix Powers

The recurrence relation for the Fibonacci numbers can be written in matrix form: whence

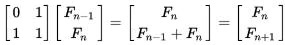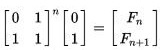and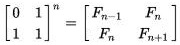

The n-th power of the matrix 2 2⍴0 1 1 1 obtains by repeated squaring and hence can be done in O(⍟n) steps.

   powop←{⍺←⊣ ⋄ ⍺∘⍺⍺{⍺⍺⍣⍵⊢⍵⍵}⍵¨⍵⍵}

   fib6←{0 1⌷⊃+.×/+.×⍨powop(⍸⌽2⊥⍣¯1⊢⍵)∘.∨⍨⍳2}

   fib6¨ 1↓⍳10
1 1 2 3 5 8 13 21 34

fib6 does not work for 0 .

If APL were extended so that:

• the power operator ⍣ accepts non-scalar right operands
• ⊤⍵ is binary representation, {2⊥⍣¯1⊢⍵}

   fib6a←{0 1⌷⊃+.×/+.×⍨⍣(⍸⌽⊤⍵)∘.∨⍨⍳2}

Because of the limited precision of 64-bit IEEE floating-point numbers this method is good only for n up to 78. But the algorithm is valid for extended precision integers. In J:

   fib6 800
692830818642247171362900776813285182733991243852048207189660
      405976914355872783831122771619675325306753741708574047
      43017623467220361778016172106855838975759985190398725

Binet’s Formula

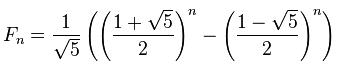
Binet’s formula derives by solving for the roots of the characteristic polynomial (x*2)-x+1 and then finding coefficients for (fib ⍵)=(a×r0*⍵)+(b×r1*⍵) which satisfy the initial conditions. The roots are the golden ratio 2÷⍨1+5*0.5 and its negative reciprocal 2÷⍨1-5*0.5 . Therefore:

   fib7←{r÷⍨-/⍵*⍨2÷⍨1+1 ¯1×r←5*0.5}

   fib7¨ ⍳10
0 1 1 2 3 5 8 13 21 34

The algorithm can be implemented using integers operations without use of √5, by doing the calculations in the ring extensions Q[√5] and Z[√5]. The powers can be done by repeated squaring and therefore the algorithm is O(⍟n) .

Rewrite Rules

Based on a suggestion by Viktor Cerovski [104], the rewrite rules 0→1 and 1→0 1 are applied n times, starting with 0 . The sum of the resulting sequence is the n-th Fibonacci number.

   fib8←{+/ ∊∘(↓∘0 1¨)∘~⍣⍵ ,0}

   fib8¨ ⍳10
0 1 1 2 3 5 8 13 21 34

Appeared in [43]