37. Gray Code

{(0∘, ⍪ 1∘,∘⊖)⍣⍵⍉⍪⍬}

Gray code encodes integers as boolean lists so that code words for adjacent numbers differ by 1 bit. For example, the 4-bit encodings of 7 and 8 are:

0 1 0 0
1 1 0 0

The 2*n Gray codes of length n can be computed as follows:

   G←{(0∘, ⍪ 1∘,∘⊖)⍣⍵⍉⍪⍬}

   G¨ 2 3 4
┌───┬─────┬───────┐
│0 0│0 0 0│0 0 0 0│
│0 1│0 0 1│0 0 0 1│
│1 1│0 1 1│0 0 1 1│
│1 0│0 1 0│0 0 1 0│
│   │1 1 0│0 1 1 0│
│   │1 1 1│0 1 1 1│
│   │1 0 1│0 1 0 1│
│   │1 0 0│0 1 0 0│
│   │     │1 1 0 0│
│   │     │1 1 0 1│
│   │     │1 1 1 1│
│   │     │1 1 1 0│
│   │     │1 0 1 0│
│   │     │1 0 1 1│
│   │     │1 0 0 1│
│   │     │1 0 0 0│
└───┴─────┴───────┘

Gray codes and the binary representations are closely related: The binary representations of n bits can be computed similarly, and one can be transformed into the other readily:

   B←{(0∘, ⍪ 1∘,)⍣⍵⍉⍪⍬}

   (B {⍺⍵} G) 3
┌─────┬─────┐
│0 0 0│0 0 0│
│0 0 1│0 0 1│
│0 1 0│0 1 1│
│0 1 1│0 1 0│
│1 0 0│1 1 0│
│1 0 1│1 1 1│
│1 1 0│1 0 1│
│1 1 1│1 0 0│
└─────┴─────┘

   (B 3) ≡ ≠\ G 3
1
   (G 3) ≡ ≠\⍣¯1 ⊢B 3
1

   (B ≡ {(⍵⍴2)⊤⍤1 0⍳2*⍵}) 8
1

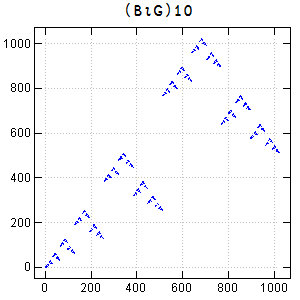
The binary base spectra [105] of G and B look like this:

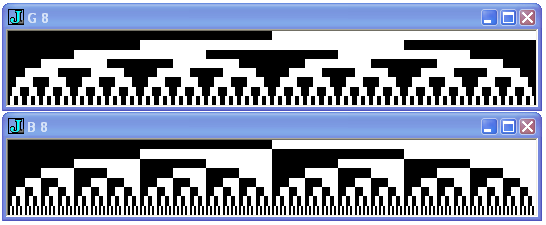
Appeared in J in [106]